4.1.8. Логические критерии пропорциональности

Попробуем теперь описать критерии, с помощью которых можно оценивать различные методы распределения мандатов и получаемые с их помощью результаты распределения. Эти критерии могут быть двух типов. Первый тип, который мы рассмотрим вначале, – логические критерии. Это правила, которые в конкретном случае либо выполняются, либо не выполняются. Для исследуемых методов правило может либо всегда выполняться, либо всегда не выполняться, либо выполняться в части случаев.

В подразделе 4.1.4 мы уже познакомились с одним из логических критериев – правилом квоты. Согласно этому правилу, каждая партия должна получить число мест, равное ее «идеальному частному», округленному либо до ближайшего большего, либо до ближайшего меньшего целого. Мы отметили, что все методы квот, использующие квоту Хэйра, это правило не нарушают, поскольку оно лежит в основе этих методов. А любой из методов делителей правило квоты способен нарушить[480].

Однако на практике ситуация у разных методов сильно различается. Так, мы анализировали действие четырех методов делителей (д’Ондта, Сент-Лагю, датского и Империали) на примере итогов голосования на 11 российских региональных выборах, прошедших в период 2004–2007 годов, где к распределению мандатов были допущены шесть списков. Оказалось, что методы Сент-Лагю и датский ни разу в рассматриваемых примерах не приводили к нарушению правила квоты; метод д’Ондта приводил к его нарушению в одном случае (тот самый пример выборов в Республике Алтай 2006 года, рассмотренный нами в подразделе 4.1.4). А вот метод делителей Империали приводил к нарушению правила квоты во всех 11 случаях, причем в одном случае оно нарушалось сразу для двух списков[481]. Отмечалось также, что если бы метод Уэбстера (Сент-Лагю) использовался для распределения мест в Палате представителей американского Конгресса с 1794 по 2002 год, он ни разу не привел бы к нарушению правила квоты[482].

В США, где анализировалось пропорциональное распределение мест между штатами, было выявлено три парадокса, характерных для метода Гамильтона (Винтона), более известного у нас под именами метода наибольших остатков и метода Хэйра – Нимейера. «Парадокс Алабамы» заключается в том, что добавление одного места в парламенте уменьшает число мест у какого-то штата; он впервые проявился в 1882 году, когда выяснилось, что увеличение числа мест в Палате представителей с 299 до 300 приводит к тому, что штат Алабама теряет одно место (вместо 8 мест получает 7). «Парадокс населения» проявляется в том, что перераспределение неизменного числа мест вследствие роста населения[483] может привести к тому, что мандат переходит от штата с относительно большим ростом к штату с относительно меньшим ростом (так, в 1902 году применение метода Гамильтона привело бы к переходу одного места от Вирджинии к Мэну, несмотря на то что за предшествующие 10 лет в процентном отношении население Вирджинии выросло больше, чем население Мэна). Третий парадокс, «парадокс нового штата», был открыт в 1907 году, когда к США присоединился штат Оклахома и одновременно число мест в Палате представителей было увеличено на 5 (что соответствовало доле Оклахомы в населении США). Оказалось, что применение метода Гамильтона в этом случае привело бы к переходу одного места от Нью-Йорка к Мэну[484].

В 1980 году М. Балинский и П. Янг доказали теорему, согласно которой никакой метод распределения не может всегда удовлетворять правилу квоты и при этом никогда не приводить к парадоксам[485]. Как уже отмечалось, метод Гамильтона (Винтона, Навилля, Хэйра – Нимейера) не нарушает правила квоты, но может приводить к парадоксам; методы делителей не приводят к парадоксам, но могут нарушать правило квоты (хотя для метода Сент-Лагю такое нарушение на практике обычно не встречается).

По нашему мнению, парадоксы Алабамы и нового штата не имеют особого значения при решении задачи о пропорциональном распределении мандатов между партиями по итогам голосования, поскольку в этом случае число распределяемых мандатов заранее фиксируется. Что касается «парадокса населения», то применительно к данной задаче он должен быть сформулирован иначе: при добавлении голосов в пользу нескольких партий мандат переходит от партии с относительно большим ростом числа голосов к партии с относительно меньшим ростом. Такая ситуация возможна, когда к участию в выборах привлекается какая-то дополнительная группа избирателей или, например, решается вопрос о действительности итогов голосования на определенном избирательном участке или группе участков.

Рассмотрим, каким образом этот метод приводит к «парадоксу населения». Представим гипотетическую ситуацию: партия А получила 460 голосов, партия Б – 244 голоса, партия В – 196 голосов; распределяется 21 мандат. Распределим мандаты по методу Хэйра – Нимейера. Квота Хэйра равна 42,86. Результаты расчета представлены в верхней части таблицы 4.15.

Таблица 4.15. Гипотетический пример проявления «парадокса населения» на выборах

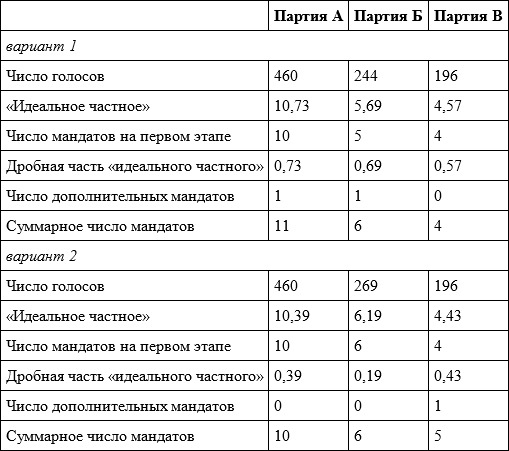
Увеличим теперь результат партии Б на 25 голосов. Квота Хэйра увеличивается до 44,05. Результаты распределения приведены в нижней части таблицы 4.15.

Итак, мы видим, что увеличение числа голосов за партию Б привело к передаче мандата от партии А к партии В. В этом и состоит суть парадокса. Происходит он из-за того, что с увеличением квоты Хэйра у партий, которые не получили дополнительных голосов, уменьшаются идеальные частные. Но у партии-лидера это приводит к большему уменьшению дробной части «идеального частного», чем у партии-аутсайдера. Поэтому если в первом случае дробная часть у партии А была больше, чем у партии В, то во втором случае уже наоборот. А партия Б не получает при этом дополнительного мандата, несмотря на повышение ее поддержки, поскольку она ранее получила шестой мандат с «большим запасом».

Результат, приведенный в таблице 4.15, не изменится и в том случае, если партия А получит еще 2 дополнительных голоса (дробная часть у партии А увеличится до 0,41, а у партии В уменьшится до 0,42). Но в этом случае может возникнуть ощущение, что дополнительные голоса, полученные партией А, привели к потере ею мандата. Однако это не так. Потеря партией А мандата связана исключительно с увеличением поддержки партии Б.

Приведенные рассуждения имеют принципиальное значение. Если бы парадокс состоял в том, что дополнительные голоса, полученные партией, могут привести к потере ею мандата, это означало бы нарушение принципа монотонности, что создает реальные возможности для манипулирования. Однако метод Хэйра – Нимейера принцип монотонности никогда не нарушает. Это обусловлено тем, что увеличение числителя (в данном случае – числа полученных партией голосов) и знаменателя (в данном случае – суммарного числа голосов за партии, участвующие в распределении мандатов) на одинаковую величину приводит к увеличению частного во всех случаях, когда числитель меньше знаменателя и все числа положительные.

«Парадокс населения» означает нарушение принципа независимости от посторонних альтернатив, поскольку при этом число голосов за одну партию влияет на распределение мандатов между двумя другими. И хотя нарушение данного принципа также дает некоторые возможности для манипулирования, эти возможности значительно меньше, чем в случае нарушения принципа монотонности. Можно даже сказать, что эти возможности минимальны в реальной ситуации, поскольку результат зависит от ряда случайных факторов, которые заранее невозможно предсказать.

Нарушение принципа независимости от посторонних альтернатив еще лучше видно на примере реальной ситуации, которую мы можем назвать «красноярским парадоксом». Он имел место на выборах в Красноярский горсовет 2 марта 2008 года, где по единому избирательному округу распределялось 17 мандатов. На этих выборах действовал 5-процентный заградительный барьер, который преодолели четыре партии – «Единая Россия», КПРФ, ЛДПР и «Справедливая Россия». Две партии («Гражданская сила» и Демократическая партия России) получили менее 2 %.

Если бы заградительного барьера не было и мандаты распределялись между шестью участвовавшими в выборах партиями (суммарное число голосов – 363 905, квота Хэйра – 21 406,176), «Гражданская сила» и ДПР все равно не получили бы ни одного мандата, но «Единой России» достались бы 8 мандатов, а «Справедливой России» – 3 мандата (см. верхнюю часть таблицы 4.16). Однако в соответствии с законом мандаты распределялись между четырьмя партиями, преодолевшими барьер (суммарное число голосов – 353 324, квота Хэйра – 20 783,765), и распределение оказалось другим: у «Единой России» дробная часть выросла с 0,360 до 0,611, и она получила дополнительный мандат за счет «Справедливой России», у которой дробная часть выросла меньше – с 0,466 до 0,540 (см. нижнюю часть таблицы 4.16).

Таблица 4.16. Результаты распределения мандатов на выборах Красноярского горсовета 2008 года по методу Хэйра – Нимейера с заградительным барьером и без него

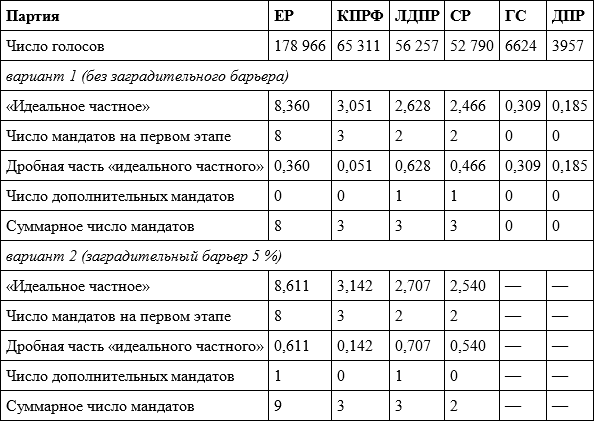
Таким образом – и в этом суть «красноярского парадокса», – добавление к участию в распределении мандатов партий, не получающих мандатов по результатам распределения, влияет на результат распределения. У методов делителей такой парадокс невозможен: там частные, которые меньше распределителя, не влияют на ранг частных, определяющих получение мандатов.

Нами был предложен еще один логический критерий, который мы назвали «правилом идеальных частных». Суть его состоит в следующем: поскольку методы распределения призваны решать проблему оптимального округления чисел в том случае, когда провести пропорциональное распределение в целых числах невозможно, то в обратном случае (когда возможно без округления распределить мандаты в точном соответствии с пропорцией голосов) они должны давать именно пропорциональный результат. Иными словами, если при делении числа голосов каждой партии на квоту Хэйра получается целое число, то именно это число мандатов данная партия должна получить при применении метода, претендующего на звание пропорционального. Мы полагаем, что только методы, которые всегда удовлетворяют данному правилу, могут считаться методами пропорционального распределения. Как показал анализ, данное правило всегда выполняется для всех известных методов распределения, за исключением одного – метода делителей Империали. Причем данный метод нарушает «правило идеальных частных» во всех случаях, когда результат лидера более чем вдвое превосходит результат аутсайдера (из числа партий, участвующих в распределении мандатов). Стоит заметить также, что аналогичные свойства будут наблюдаться у любого метода делителей, в котором шаг между делителями (если привести ряд делителей к форме, когда он начинается с единицы) будет меньше единицы[486].