4.1.5. Другие истинные методы делителей

Как отмечалось в подразделе 4.1.3, истинные методы делителей различаются между собой правилами округления. Все остальные различия – производные от этого главного.

Вернемся теперь к американской истории. После того как в 1832 году был выявлен недостаток метода Джефферсона, который заключался в возможности нарушения правила квоты, Конгрессу были предложены два альтернативных метода делителей – один предложил бывший президент Дж. К. Адамс, другой – конгрессмен Д. Уэбстер. Предпочтение было отдано методу Уэбстера (в Европе этот метод позднее получил имя А. Сент-Лагю). Метод Уэбстера был использован в 1842 году, затем от него отказались, но в 1902 году к нему вернулись. Однако вскоре статистик Дж. Хилл и математик Э. Хантингтон предложили еще один метод (его называют либо методом Хантингтона – Хилла, либо просто методом Хилла). И с 1932 года места между штатами США распределяются по этому методу[449].

Известен также метод Дина, примеры применения которого на практике нам неизвестны[450]. Позднее появился метод, получивший название датского: он используется в Дании для распределения дополнительных мандатов между округами внутри региона[451].

Как отмечалось в предыдущем подразделе, метод Джефферсона (д’Ондта) подразумевает округление частных от деления результата партии на распределитель до ближайшего меньшего целого. В противоположность ему метод Адамса предполагает округление до ближайшего большего целого. Метод Уэбстера (Сент-Лагю) предусматривает округление по стандартному правилу: числа с дробной частью менее 0,5 округляются до ближайшего меньшего целого, а с дробной частью 0,5 и более – до ближайшего большего целого. Иными словами, здесь рубежом является среднее арифметическое между ближайшими меньшим и большим целыми.

Еще два метода в качестве такого рубежа используют другие средние: метод Хантингтона – Хилла – среднее геометрическое, метод Дина – среднее гармоническое. Датский метод использует в качестве рубежа одну треть: числа с дробной частью менее ? округляются до ближайшего меньшего целого, а с дробной частью ? и более – до ближайшего большего целого.

Для реализации всех этих методов в принципе возможны те же четыре алгоритма, которые описаны в подразделе 4.1.3 для метода Джефферсона (д’Ондта). Однако в некоторых случаях возникают технические сложности.

Наиболее проста реализация всех алгоритмов для методов Уэбстера (Сент-Лагю) и датского. Для первого получается ряд делителей 0,5; 1,5; 2,5; 3,5 и т. д. (первый делитель – среднее арифметическое между 0 и 1, второй – среднее арифметическое между 1 и 2 и т. д.). Обратим, однако, внимание на замечательный факт: если мы все делители умножим на один и тот же коэффициент, ранжировка полученных частных от этого не изменится. А нас при реализации третьего алгоритма интересует исключительно ранжировка. Поэтому для метода Сент-Лагю принято использовать третий алгоритм с удвоенным рядом делителей: 1, 3, 5, 7 и т. д.

Подобным же образом преобразуется третий алгоритм для датского метода. Исходный ряд делителей – ?, 1?, 2?, 3? и т. д. Умножая все делители на 3, получаем ряд, который используется на практике: 1, 4, 7, 10 и т. д.

Покажем, как работает метод Сент-Лагю, на брюссельском примере. Начнем с алгоритмов 3 и 4, которые иллюстрирует таблица 4.9.

Таблица 4.9. Распределение мандатов по итогам голосования в брюссельском округе на выборах бельгийского парламента 1900 года с использованием метода Сент-Лагю

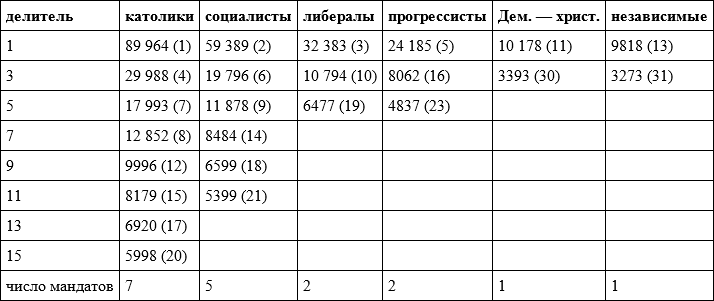
Примечание: в скобках – порядковый номер числа в убывающем ряду.

Итак, мы видим, что в рамках четвертого алгоритма мандаты распределяются в несколько иной последовательности, чем в случае метода д’Ондта. Первые два мандата также получают католики и социалисты, но третий мандат в этом случае достается либералам. Четвертый мандат получают католики, пятый – прогрессисты и так далее. Последний, 18-й мандат получают социалисты. В целом же распределение оказывается таким же, как и у метода Навилля (Хэйра – Нимейера): 7:5:2:2:1:1.

Кстати, если использовать второй алгоритм, то нужно либо делить на ряд 0,5; 1,5; 2,5 и т. д., либо умножить частное с порядковым 18-м номером на два. В обоих случаях получаем число, которое следует округлить вниз до 13 197 – это и будет распределитель (точнее, его максимально возможное значение). С помощью первого алгоритма (то есть подбора) можно выяснить, что искомым распределителем может быть любое число в сегменте от 12 954 до 13 197. Как видим, этот распределитель в данном случае больше квоты Хэйра.

Что касается методов Хилла и Дина, то для них использование второго, третьего и четвертого алгоритмов затруднено тем, что ряд делителей не получается простым и запоминающимся. К тому же у метода Хилла это в основном иррациональные числа, например второй делитель – ?2, третий – ?6 и т. д. Кроме того, у этих методов, а также у метода Адамса главная проблема с первым делителем: у метода Адамса он должен быть нулем, но на ноль делить нельзя; у методов Хилла и Дина – соответственно среднее геометрическое и среднее гармоническое 0 и 1, а они не существуют (или их с некоторой натяжкой можно приравнять к нулю). Формально это означает, что первое частное у всех партий (или у всех штатов) получается бесконечно большим, то есть каждой партии (или каждому штату) следует вначале дать по одному мандату. В случае распределения мест между штатами это нормально: каждый штат должен получить хотя бы одно место. Но в приложении к распределению мандатов между партиями по итогам голосования такой подход может привести к получению мандатов партиями, за которые проголосовало ничтожное число избирателей. Неудивительно, что методы Адамса, Хилла и Дина не применяются для распределения мандатов при пропорционально-списочных системах (хотя, как мы увидим дальше, отмеченная проблема снимается с помощью заградительного барьера).

Тем не менее все эти методы имеют определенный смысл. Если метод Джефферсона (д’Ондта) исходит из принципа: мандат дается той партии, у которой его «цена» после получения будет наибольшей, то у метода Адамса принцип альтернативный: мандат надо давать той партии, у которой на данный момент «цена» мандата наибольшая. Методы Уэбстера (Сент-Лагю), Хилла и Дина предусматривают различные средние варианты между этими двумя альтернативами. Что касается датского метода, то это некое упрощение методов Хилла и Дина – чтобы не иметь дело со сложными формулами и тем более иррациональными числами.

В обобщенном виде свойства методов делителей представлены в таблице 4.10.

Таблица 4.10. Свойства различных методов делителей

Примечание: s – число мандатов, уже полученных партией.

Для любого из истинных методов делителей может быть предложен соответствующий ему метод квот – аналогично методу д’Ондта. Он будет состоять в том, что после первичного распределения мандатов оставшиеся нераспределенными мандаты распределяются по определенному правилу: результат партии делится на определенный делитель и полученные частные округляются по определенному правилу (см. таблицу 4.10).

Поскольку термин «правило наибольшей средней» исторически закреплен за вариантом, соответствующим методу д’Ондта, мы, чтобы не было путаницы, будем называть это более общее правило правилом «наибольшего частного»[452].

В целом указанные методы имеют в основном теоретическое значение, так как для большинства из них нет примеров применения на практике. Однако, как будет показано в подразделе 4.1.9, у некоторых из них есть важные достоинства.

Отдельная проблема для методов квот, соответствующих методам Адамса, Хилла и Дина: что делать с партиями, у которых s=0? Разумеется, на ноль делить нельзя, поэтому наиболее простой вариант – дать партиям, еще не получившим мандатов, мандаты в первую очередь[453].

В брюссельском примере ни один из рассмотренных выше методов делителей правило квоты не нарушает, поэтому распределение мандатов с помощью этих методов совпадает с распределением мандатов с помощью соответствующих методов квот, основанных на правиле «наибольшего частного». В связи с этим в таблице 4.11 на брюссельском примере приводятся более наглядные расчеты для методов квот. Для демохристиан и независимых расчеты не показаны, но методы, соответствующие методам Сент-Лагю и датскому, также дают им по мандату в первую очередь.

Как видим, методы среднего арифметического и среднего геометрического (Сент-Лагю и Хилла) дают такое же распределение, как и метод Навилля (Хэйра – Нимейера), а три других метода – иное распределение, которое по сравнению с методом Навилля дает дополнительный мандат либералам за счет социалистов.

Таблица 4.11. Распределение мандатов по итогам голосования в брюссельском округе на выборах бельгийского парламента 1900 года с использованием различных вариантов правила «наибольшего частного»

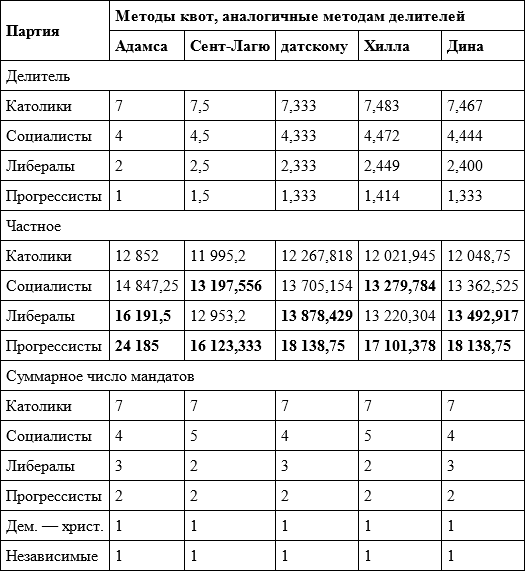
Примечание: жирным шрифтом выделены два наибольших (для соответствующего метода) частных, дающих партии дополнительный мандат.