5.2. Индексы диспропорциональности

Как отмечалось выше (см. главу 4), практически невозможно распределить мандаты так, чтобы соотношение переданных партиям мандатов абсолютно точно соответствовало соотношению полученных ими голосов избирателей. Кроме того, пропорциональность распределения искажается наличием заградительного барьера и других специальных норм, на нее влияют размер избирательного округа, методика распределения мандатов и другие факторы. В связи с этим возникла необходимость определить показатели, которые давали бы оценку степени отклонения конкретного распределения мандатов от строгой пропорциональности.

Такие показатели получили название индексов диспропорциональности[676]. Все они основаны на модуле разности между долей голосов, поданных за партию (от числа действительных бюллетеней), и долей полученных ею мандатов |v_i – s_i|. Наиболее простым показателем является максимальное отклонение: MD = max |v_i – s_i|. Оно показывает верхний предел искажений пропорциональности.

В качестве примера с помощью таблицы 5.10 приведем расчеты индексов диспропорциональности для выборов депутатов Совета народных депутатов г. Новозыбков Брянской области, прошедших по пропорциональной системе 14 сентября 2014 года, где распределялось 25 мандатов по тюменскому методу (см. подраздел 4.1.6). Наибольшим модуль разности получился у «Единой России» – 6,0 %, это и есть максимальное отклонение.

Таблица 5.10. Данные для расчета индексов диспропорциональности на примере выборов депутатов Совета народных депутатов г. Новозыбков Брянской области 14 сентября 2014 года

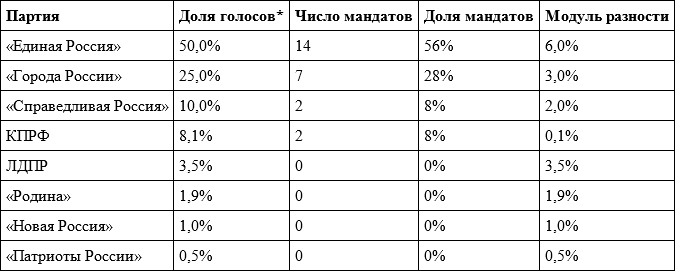
* От числа действительных голосов.

Другие показатели учитывают искажения представительства всех партий, участвовавших в выборах. Первым был предложен индекс Рэ, который равен сумме модулей всех отклонений, деленной на число участвовавших в выборах партий: I = ?|v_i – s_i| / n. В нашем случае указанная сумма равна 18,1 % и соответственно индекс Рэ равен этому числу, деленному на 8, то есть 2,3 %.

Таким образом, индекс Рэ показывает среднее искажение представительства партий. Однако для сравнительных исследований он неудобен из-за высокой чувствительности к числу партий-аутсайдеров, практически не влияющих на результат выборов. Например, если в наш случай добавить еще всего одну партию, приписав ей 0,1 % голосов, индекс Рэ снизится до 2,0 %.

Для смягчения этого недостатка был предложен индекс Грофмана: для его расчета сумма модулей всех отклонений делится на эффективное число партий (см. раздел 5.1). В нашем примере это число равно 3,03; соответственно индекс Грофмана получается равным 6,0 %.

Для сравнительных исследований все же более удобны показатели, не зависящие от числа участвующих в выборах партий. Таков, в частности, индекс Лузмора – Хэнби, о котором уже шла речь в подразделе 4.1.9. Он равен ? ?|v_i – s_i|. Этот индекс показывает долю избирателей, чьи предпочтения были искажены при распределении мандатов: в данном контексте деление на двойку отражает то обстоятельство, что сумма модулей отклонений учитывает искажения предпочтений одних и тех же избирателей дважды (в плюс и в минус). В нашем примере индекс Лузмора – Хэнби равен 9,0 %.

В качестве недостатка индекса Лузмора – Хэнби отмечается, что он не делает различий между случаем, когда суммарное искажение определяется большими отклонениями у одной-двух партий, и случаем, когда такое же искажение получается в результате суммирования большого числа мелких отклонений. Для преодоления этого недостатка был предложен индекс Галлахера, который основан на среднеквадратичном отклонении: LSq = ? ? ?(v_i – s_i)². Этот индекс в большей степени учитывает сильные искажения и менее чувствителен к слабым. В нашем примере индекс Галлахера равен 5,8 %.

С другой стороны, у индекса Лузмора – Хэнби есть определенные преимущества перед индексом Галлахера. Помимо простоты и наглядности стоит отметить также то, что для вычисления индекса Лузмора – Хэнби не обязательно знать результат каждой из партий-аутсайдеров: достаточно иметь суммарное число голосов (или суммарную долю голосов), поданных за все партии, не участвовавшие в распределении мандатов.

Далее мы будем использовать только два показателя – индекс Лузмора – Хэнби и индекс Галлахера. Отметим, что расчет индексов диспропорциональности возможен не только для случаев применения пропорциональной системы, но также для мажоритарной и смешанной. При этом для смешанных систем с двумя голосами у избирателя доля голосов, полученных партией, определяется на основе итогов голосования по пропорциональной составляющей, а при использовании мажоритарной системы эту долю приходится вычислять исходя из суммарного числа голосов, поданных за кандидатов от соответствующей партии.

Главную сложность здесь представляет наличие независимых кандидатов, особенно в тех случаях, когда они добиваются мандатов. Тут возможны два крайних подхода: в первом случае каждый независимый кандидат рассматривается как отдельная партия, во втором случае они все условно считаются как бы принадлежащими одной партии. Впрочем, часто эти подходы дают одинаковый результат. Однако в любом случае наличие успешных независимых кандидатов не вписывается в логику партийного представительства, на которой основаны индексы диспропорциональности. В связи с этим далее в наших примерах будут использоваться только выборы, где все мандаты получали представители политических партий, за исключением выборов депутатов Государственной Думы 1993, 1995, 1999 и 2003 годов.

Отдельного внимания заслуживают выборы германского бундестага. Как отмечалось в подразделе 3.7.2, эти выборы с 1953 года проводятся по смешанной связанной системе с двумя голосами у избирателя. Система эта (в Германии именуемая также персонализированной пропорциональной) позволяет обеспечивать довольно точное соответствие результатов распределения мандатов итогам голосования за партийные списки. Как видно из таблицы 5.11[677], в отдельных случаях индекс Лузмора – Хэнби оказывался ниже 1 %, а индекс Галлахера достигал 0,5 %.

Таблица 5.11. Индексы диспропорциональности для выборов германского бундестага

Главным источником искажений при такой системе является заградительный барьер. В Германии он составляет 5 % (но не действует для партий, выигравших не менее чем в трех одномандатных округах), однако лишь в редких случаях (1957, 1969, 1990, 2002 и 2013 годы) оказывались партии, получившие более 3 % голосов и не допущенные к распределению мандатов. И доля голосов за партии, допущенные к распределению мандатов, до 2013 года не опускалась ниже 90 %, в большинстве случаев была выше 94 %, а порой превышала 99 %. Но в 2013 году сразу две партии лишь немного не дотянули до 5-процентного барьера (получив 4,8 и 4,7 %), и это привело к резкому увеличению значений индексов диспропорциональности.

Отметим, что в условиях, когда решающую роль в искажении пропорциональности играет заградительный барьер, индекс Лузмора – Хэнби равен доле голосов за партии, не допущенные к распределению мандатов, поскольку у всех партий, получивших мандаты, их доля оказывается выше доли полученных ими голосов. Это хорошо видно из таблицы 5.11, где сумма значений во второй и третьей колонках в большинстве строк равна 100 %.

В таблице 5.12 представлены индексы диспропорциональности для выборов других зарубежных парламентов[678]. Здесь мы видим существенные различия в уровне диспропорциональности. Наилучшее приближение к пропорциональности было достигнуто в Дании и Нидерландах, что связано как с незначительной долей голосов за партии, не допущенные к распределению мандатов (здесь самые низкие заградительные барьеры), так и с правилами распределения: в Нидерландах мандаты распределяются в едином общенациональном округе, в Дании – многоуровневая система (см. подраздел 4.2.3).

Таблица 5.12. Индексы диспропорциональности для выборов зарубежных парламентов

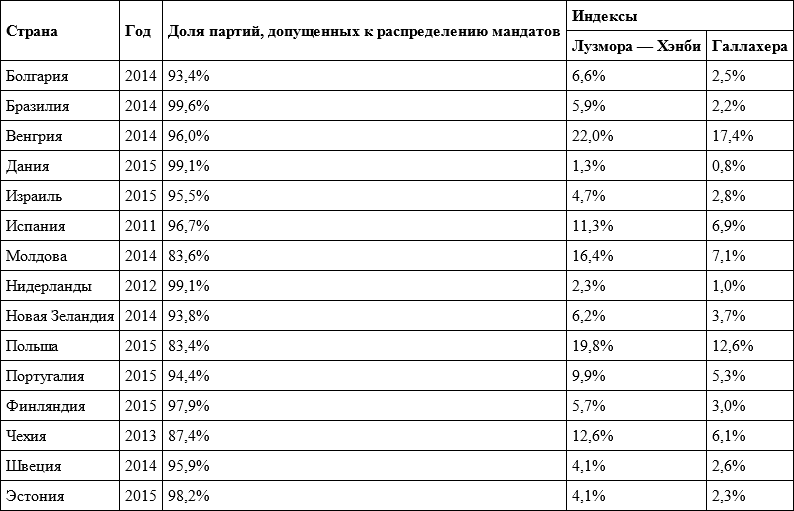
По тем же причинам невысокая диспропорциональность в Израиле, Швеции и Эстонии. Стоит также отметить достаточно низкие значения индексов диспропорциональности в Новой Зеландии, где используется смешанная связанная система, близкая к германской.

В ряде других стран степень диспропорциональности значительно выше. Если в Молдове и Чехии это связано исключительно с завышенными заградительными барьерами (как видим, здесь сумма доли партий, допущенных к распределению мандатов, и индекса Лузмора – Хэнби составляет 100 %), то в Польше к завышенным барьерам добавляется распределение мандатов на уровне небольших округов, что искажает пропорциональность. Последний фактор играет существенную роль также в Бразилии, Испании, Португалии и Финляндии. В Венгрии искажения в основном достигаются за счет мажоритарной составляющей смешанной системы.

На выборах депутатов Государственной Думы в 1993–2003 годах использовалась параллельная (смешанная несвязанная) система, при этом по одномандатным округам избиралась значительная доля непартийных кандидатов, у избирателя была возможность голосовать «против всех»[679], а 5-процентный барьер приводил к большой доле «пропадавших» голосов (см. таблицу 5.13). Все эти обстоятельства вместе взятые обуславливали существенную диспропорциональность. После перехода к пропорциональной системе (с одновременной отменой голосования «против всех») индексы диспропорциональности заметно снизились и единственным искажающим пропорциональность фактором остался заградительный барьер.

Таблица 5.13. Индексы диспропорциональности для выборов Государственной Думы

* Слева – все избранные непартийные кандидаты условно считались принадлежащими одной партии; справа – каждый избранный непартийный кандидат рассматривался как отдельная партия.

Интересно также проследить за индексами диспропорциональности на выборах Законодательного Собрания Свердловской области, поскольку они 8 раз проводились по пропорциональной системе (каждый раз избирались 14 депутатов – половина состава Областной Думы, нижней палаты Законодательного Собрания), а последний раз (в 2011 году) – по параллельной системе. Заградительный барьер до 2004 года включительно составлял 5 % от числа проголосовавших избирателей, с 2006 года он был повышен до 7 %. Голосование «против всех» практиковалось вплоть до 2006 года. Для распределения мандатов до 2008 года использовался метод Хэйра – Нимейера, а с 2008 года – тюменский метод.

Как видно из таблицы 5.14, до 2006 года основным источником искажений были заградительный барьер и голосование «против всех». В 2008 году начало сказываться также действие тюменского метода, в 2010 году, когда все четыре участвовавших в выборах партии преодолели 7-процентный барьер, главным ограничителем оказалось число распределяемых мандатов (в данном случае тюменский метод давал такой же результат, как и методы Хэйра – Нимейера и Сент-Лагю). С переходом на параллельную систему главным источником искажений стала мажоритарная составляющая.

Таблица 5.14. Индексы диспропорциональности для выборов Законодательного Собрания Свердловской области

Примечание: 1998–2010 годы – выборы Областной Думы Законодательного Собрания по пропорциональной системе; 2011 год – выборы однопалатного Законодательного Собрания по параллельной системе.

В таблицах 5.15–5.17 приведены индексы диспропорциональности для ряда региональных и муниципальных выборов, проходивших с 2007 года (а также для выборов в Московскую городскую Думу 2005 года), на которых не было голосования «против всех». Кроме того, в случае параллельной системы мы подобрали только такие выборы, где мандаты в мажоритарной части завоевали исключительно партийные кандидаты.

Как видно из таблиц 5.15 и 5.17, в случае применения пропорциональной системы при использовании метода Хэйра – Нимейера и 100-процентной доле партий, допущенных к распределению мандатов, индексы диспропорциональности могут быть крайне малыми (вплоть до 0,1 %). Однако сама по себе пропорциональная система не гарантирует от искажений: в Республике Калмыкии в 2013 году, Московской области в 2007 году, а также в г. Волжский в 2013 году из-за высокой доли голосов, поданных за партии, не преодолевшие заградительный барьер, индекс Лузмора – Хэнби превысил 20 %, а индекс Галлахера – 10 %.

Таблица 5.15. Индексы диспропорциональности для выборов российских региональных парламентов по пропорциональной системе

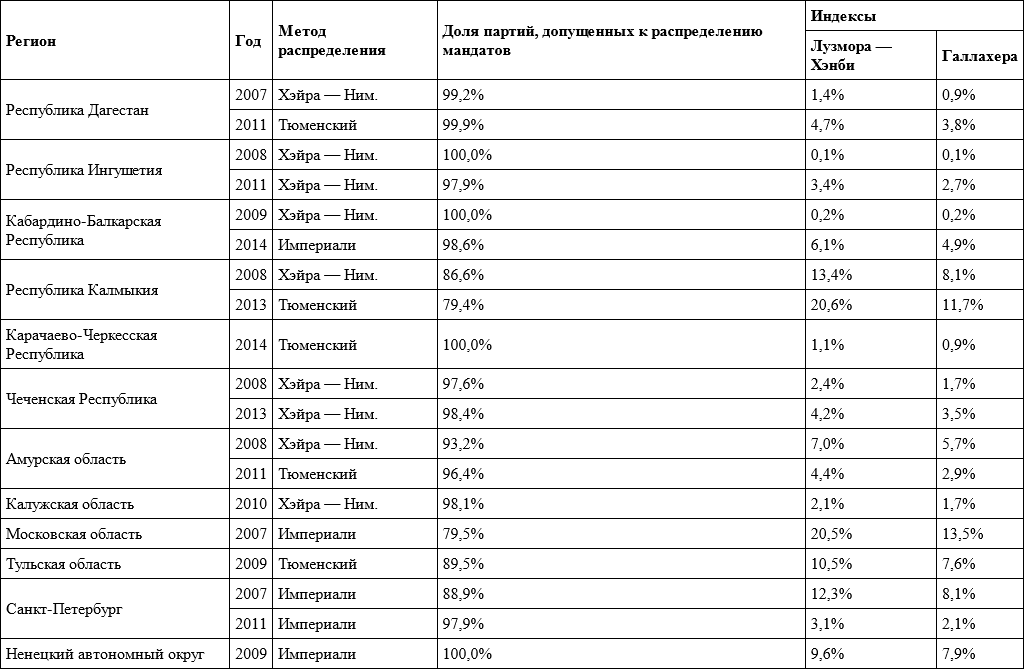
При применении параллельной системы (см. таблицы 5.16 и 5.17) искажения обычно выше. В приведенных примерах лишь в двух случаях из 37 индекс Лузмора – Хэнби был ниже 17 %, а индекс Галлахера лишь в трех случаях ниже 13 %. Наибольших значений в рассматриваемых примерах эти индексы достигли в Твери в 2012 году – 33,3 % (индекс Лузмора – Хэнби) и 25,2 % (индекс Галлахера).

Таблица 5.16. Индексы диспропорциональности для выборов российских региональных парламентов по параллельной системе

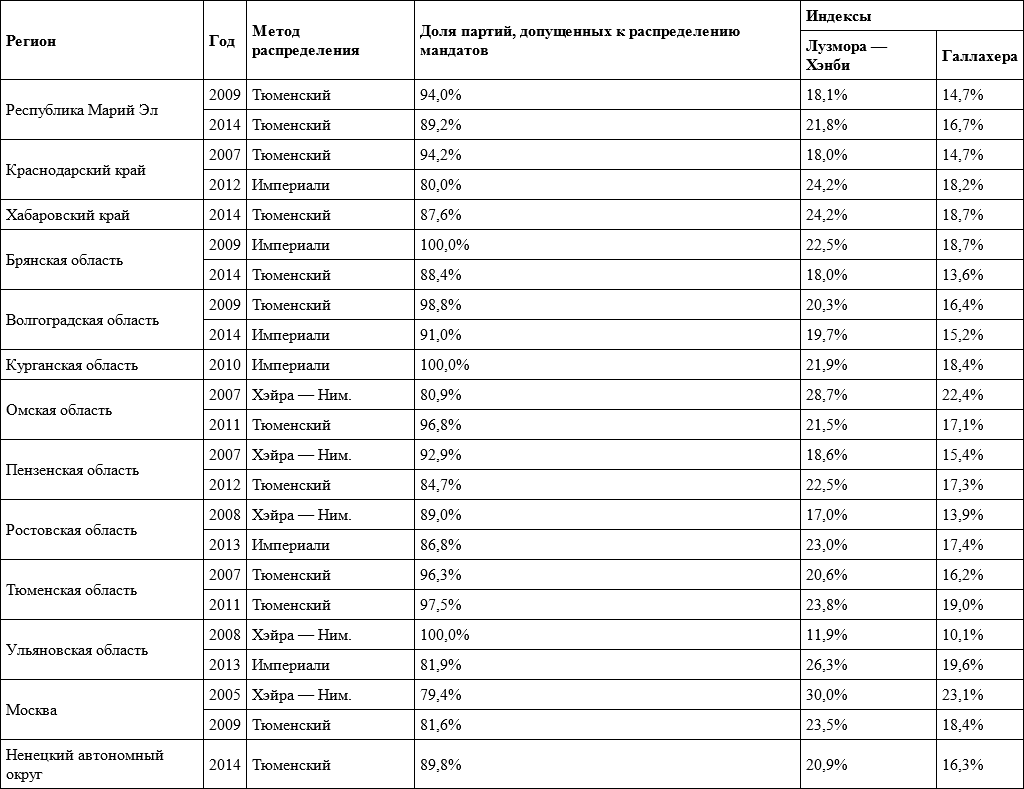
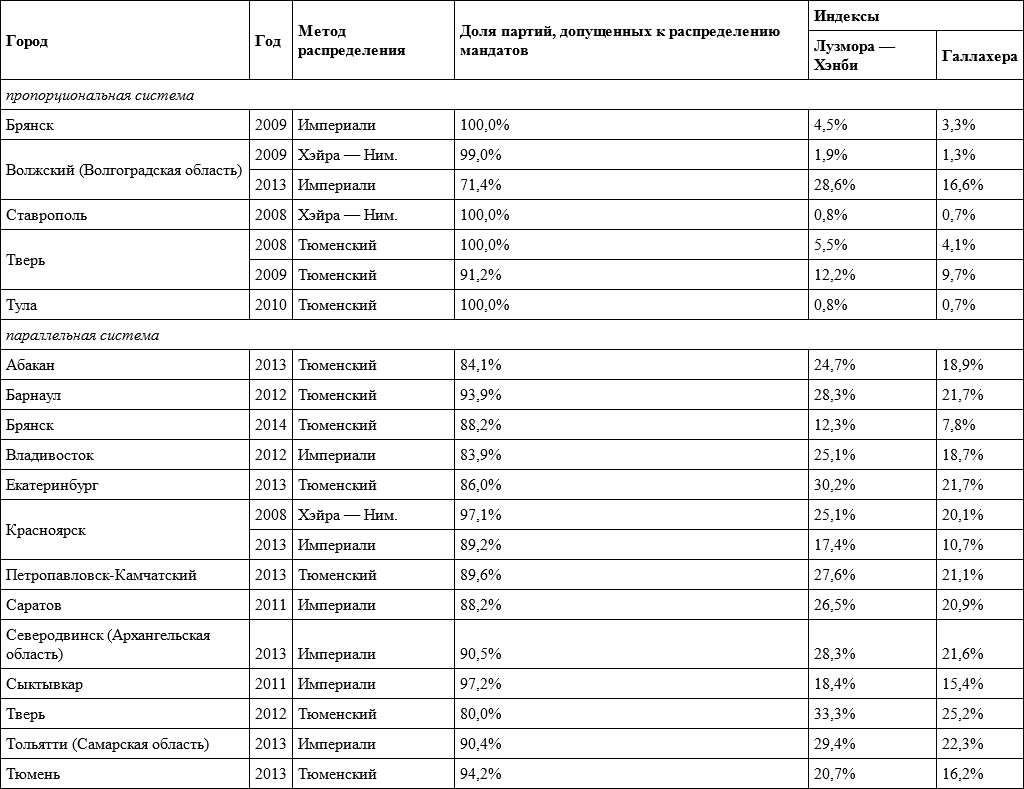
Таблица 5.17. Индексы диспропорциональности для выборов представительных органов российских городов

А. Лейпхарт на примере выборов в 27 странах в период 1945–1990 годов попытался оценить, какие факторы влияют на индексы диспропорциональности. Всего анализировалось 69 случаев, при этом каждый случай охватывал одну или несколько избирательных кампаний, если при этом не менялись основные правила (размер избирательных округов, заградительный барьер, методика распределения мандатов). Для плюральной системы (7 случаев) среднее значение индекса Галлахера получилось равным 13,6 %, для других вариантов мажоритарной системы (5 случаев) – 10,9 %, для пропорциональных систем с использованием метода д’Ондта (32 случая) – 5,2 %, с использованием метода наибольшего остатка и квоты Друпа (13 случаев) – 4,2 %, с использованием метода наибольшего остатка и квоты Хэйра (12 случаев) – 1,9 %. Регрессионный анализ показал, что наибольшее влияние на степень диспропорциональности оказывает параметр, именуемый эффективным порогом[680] (который условно определяется как среднее между порогами включения и исключения[681], см. подраздел 4.6.1, либо равен заградительному барьеру, если он установлен в законе и при этом превышает порог исключения).

Д. Мюллер приводит значения индекса Лузмора – Хэнби (а также индекса Лааксо – Таагеперы) по итогам выборов 1983–1990 годов для большого числа стран. При этом для 13 стран с одномандатными округами среднее значение индекса Лузмора – Хэнби составило 21,1 %, а для 25 стран с пропорциональной системой – 5,8 %. При этом для 8 стран с размером округа от 2 до 5 мандатов среднее значение индекса получилось равным 7,5 %, для 6 стран с размером округа от 6 до 10 мандатов – 4,9 %, для 4 стран с размером округа от 11 до 15 мандатов – 4,8 % и для 9 стран с размером округа более 15 мандатов – 5,8 %[682]. Таким образом, создается впечатление, что увеличение размера округа выше 6 не приводит к значительному снижению диспропорциональности. Однако размер выборки слишком мал, чтобы можно было делать столь серьезные выводы.