4.1.3. Метод Джефферсона (д’Ондта)

Метод Джефферсона был предложен Конгрессу США для распределения мест между штатами, когда президент страны Дж. Вашингтон наложил вето на билль, одобрявший метод Гамильтона. Он использовался до 1832 года, когда у него был обнаружен существенный недостаток[443]. Аналогичный метод для распределения мандатов между партиями предложил в 1882 году профессор Гентского университета В. д’Ондт. Этот метод стал первым из использованных методов делителей.

Как отмечалось в подразделе 4.1.1, недостаток метода Гамильтона состоит в том, что округление частных от деления на квоту происходит не по определенному правилу, а зависит от случайных факторов. Общая идея методов делителей состоит в том, чтобы найти такое число (распределитель), разделив на которое результат каждой партии (в голосах избирателей) можно было затем все частные округлить по единому правилу и в результате сразу получить распределение всех мандатов.

Самым существенным параметром для метода (а для истинных методов делителей – единственным существенным, определяющим параметром) и является правило округления. Алгоритмы нахождения необходимого распределителя могут быть различными, к тому же обычно существует не одно число, а набор чисел, удовлетворяющих условиям поиска. Но если такой распределитель найден, он приводит к однозначному распределению мандатов. Поэтому алгоритмы, всегда приводящие к одному и тому же результату, мы будем считать разными способами реализации одного и того же метода.

Принцип метода Джефферсона (д’Ондта) – округление полученных частных до ближайшего меньшего целого. Для его реализации известно как минимум четыре алгоритма. Опишем их все, и это поможет нам лучше понять и этот метод, и другие методы делителей.

Первый алгоритм, вероятно, и использовался в США в 1794–1832 годах. Он заключался в поиске нужного распределителя методом проб и ошибок (подбора). Сначала в качестве распределителя используется квота Хэйра, но она, как известно, позволяет распределить меньшее число мандатов. Затем этот распределитель каким-то образом уменьшается, и процедуры деления и округления повторяются. Если опять получилось недостаточное число мандатов, распределитель еще раз уменьшается, если большее число – увеличивается. И так до тех пор, пока не будет найдено необходимое число.

Применим этот алгоритм к примеру, приведенному в таблице 4.1. Будем постепенно уменьшать квоту Хэйра (которая округленно равна 12 551) и обнаружим, что нас удовлетворит любое число в сегменте от 10 179 до 10 794. Деление на любое из этих чисел с последующим округлением полученных частных до ближайшего меньшего целого дает нам следующее распределение 18 мандатов: католики – 8, социалисты – 5, либералы – 3, прогрессисты – 2, остальным двум партиям мандаты не достаются.

Алгоритм этот довольно трудоемок при расчетах вручную и к тому же требует хорошей интуиции. Для более быстрого и надежного нахождения распределителя В. д’Ондт предложил второй алгоритм. Он заключается в делении результатов каждой партии на последовательный ряд натуральных чисел: 1, 2, 3, 4 и т. д. (в общем случае – до числа распределяемых мандатов, но обычно этот ряд можно закончить и раньше). Затем все полученные таким образом частные (их количество в общем случае равно произведению числа партий на число мандатов) сортируются в порядке убывания и определяется частное, порядковый номер которого равен числу распределяемых мандатов. Это и будет искомый распределитель.

Проиллюстрируем этот алгоритм вновь на брюссельском примере в таблице 4.4. Здесь показано деление только на первые 9 чисел ряда: в данном случае этого оказывается достаточно.

Таблица 4.4. Распределение мандатов по итогам голосования в брюссельском округе на выборах бельгийского парламента 1900 года с использованием алгоритма д’Ондта

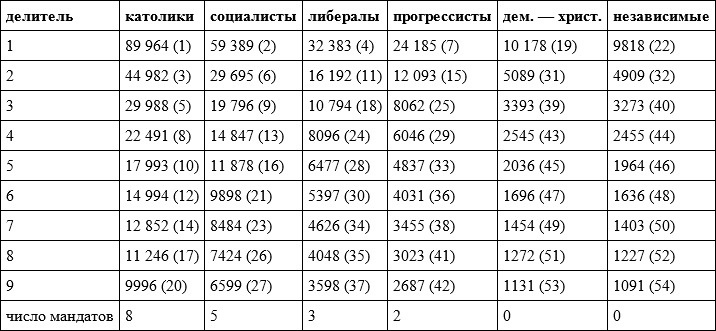
Примечание: в скобках – порядковый номер числа в убывающем ряду.

Как видно из таблицы, нужный нам 18-й номер имеет число 10 794 (частное от деления результата либералов на 3), которое совпадает с максимальным значением распределителя, найденного нами с помощью первого алгоритма. И мы уже знаем, что деление результатов партий на это число дает нам распределение 8:5:3:2:0:0.

Глядя на таблицу 4.4, нетрудно догадаться, что второй алгоритм можно упростить на конечном этапе. На самом деле нет необходимости делить результаты каждой партии на найденный распределитель, то есть совершать дополнительные операции деления (в данном случае 6 дополнительных операций). Из таблицы легко увидеть, что у католиков есть 8 частных, которые больше найденного нами распределителя (или, что то же самое, порядковый номер которых меньше 18). У социалистов таких частных – 5, у либералов – 3 (включая частное, равное распределителю), у прогрессистов – 2, у остальных таких частных нет. Таким образом, можно сформулировать третий алгоритм: результаты каждой партии делятся на ряд натуральных чисел; полученные частные ранжируются в порядке убывания, и партия получает столько мандатов, сколько ее частных имеют номер, который меньше числа распределяемых мандатов или равен ему.

Хотя в Российской Федерации метод д’Ондта в чистом виде не применяется (он применялся лишь в Республике Калмыкии в 2003 году), при использовании других методов делителей законы обычно описывают именно такой алгоритм – он вполне удобен для нормативного описания. Также он удобен для расчетов в Excel’е.

Однако описываемый далее четвертый алгоритм не только делает менее трудоемким ручной расчет, но и позволяет лучше понять сущность метода д’Ондта и других методов делителей.

Алгоритм заключается в последовательном распределении каждого мандата. И на каждом шаге определяется, какой партии «по справедливости» должен достаться новый мандат.

С первым мандатом вопросов нет: его надо дать партии, получившей наибольшее количество голосов. Но уже со вторым мандатом нужно решать: дать его той же партии или партии, занявшей второе место. Нужен критерий, и в качестве такого критерия выступает отношение числа полученных партией голосов к числу уже полученных ею мандатов плюс один: v/(s+1). Иными словами, мандат дается той партии, у которой его «цена» после получения будет наибольшей.

И вновь для иллюстрации обратимся к таблице 4.4. Первый мандат получают католики. Второй – социалисты: у них частное от деления результата на 1 (то есть на 0+1) больше, чем частное от деления результата католиков на 2 (то есть на 1+1). Третий мандат отходит католикам: теперь у них частное от деления результата на 2 больше как частного от деления результата социалистов на 2, так и частного от деления результата либералов на 1.

И так далее. Собственно, порядковые номера, указанные в таблице 4.4, показывают нам всю последовательность распределения 18 мандатов. Четвертый мандат получают либералы, пятый – католики, шестой – социалисты, седьмой – прогрессисты, восьмой – католики, девятый – социалисты. И так мы распределяем все 18 мандатов. При таком алгоритме нам не нужно делить результат католиков больше чем на 9, результат социалистов – больше чем на 6, результат либералов и прогрессистов – больше чем на 3, а результаты демохристиан и независимых вообще не нужно делить. И главное – ясен принцип: давать мандат в каждый момент тем, у кого «цена» мандата будет больше.

Б. А. Велихов уподобил данный алгоритм аукциону, где платежными единицами являются голоса и каждый следующий мандат «продается» той партии, которая может «оплатить» этот и ранее полученные мандаты большим числом голосов из расчета на один мандат[444].

Итак, все алгоритмы метода д’Ондта приводят нас к распределению 8:5:3:2:0:0. Как показано в предыдущих подразделах, метод Навилля (Хэйра – Нимейера) дает распределение 7:5:2:2:1:1, а метод, основанный на квоте Империали и правиле наибольшего остатка, дает распределение 8:5:2:2:1:0. Какое из них более справедливое, мы обсудим в подразделе 4.1.9.