5.1. Показатели конкуренции и фрагментации

Исследователям часто необходимо оценить степень конкуренции на прошедших выборах, а также степень фрагментации партийного спектра. При этом важно иметь возможность выразить такую степень в виде единого числового показателя, чтобы можно было сравнивать между собой различные выборы (выборы в разных странах, в разных регионах, а также на одной и той же территории в разные годы).

Такой показатель получил название эффективного числа партий (ЭЧП)[671], а для выборов, в которых участвуют индивидуальные кандидаты, – эффективного числа кандидатов (ЭЧК). Формулы для ЭЧП и ЭЧК одинаковы, поскольку они имеют один и тот же смысл. Предложено несколько вариантов расчета этих показателей. Наибольшее употребление нашел индекс Лааксо – Таагеперы, который рассчитывается по формуле: 1/?n_i², где n_i – доля голосов, полученных i-й партией или i-м кандидатом. Здесь важно подчеркнуть, что доля эта должна считаться от числа голосов, поданных за всех кандидатов или за все партии, поскольку принципиально важно, чтобы сумма всех n_i равнялась единице. Если голосование категорическое и у избирателя нет возможности голосовать «против всех», то число голосов, поданных за всех кандидатов или за все партии, равно числу действительных бюллетеней, а это число обычно включается в официальные данные об итогах голосования.

Важным свойством индекса Лааксо – Таагеперы является то, что в случае, если все кандидаты (партии) получили одинаковое число голосов, он получается равным просто числу этих кандидатов (партий). Если, как это обычно происходит, они получают неравное число голосов, индекс Лааксо – Таагеперы меньше их числа. Если один из кандидатов (одна из партий) получает результат, близкий к 100 %, то индекс Лааксо – Таагеперы оказывается близким к 1. Если одна из партий разделяется на две или больше, а результат других партий при этом не изменяется, то значение индекса увеличивается. Эти свойства делают индекс Лааксо – Таагеперы понятным и близким к интуитивным представлениям о степени конкуренции и фрагментации.

Однако в адрес этого индекса высказываются и критические замечания. Одно из них состоит в том, что его значения расходятся с интуитивными оценками, давая завышенные значения, в тех случаях, когда результат лидера превышает 50 %, что часто имеет место в странах, где доминирует одна партия. В связи с этим были предложено еще несколько вариантов расчета ЭЧП и ЭЧК, среди которых наиболее интересен индекс, предложенный Г. В. Голосовым. Он рассчитывается по формуле ?{1/[1+(n₁²/n_i) – n_i]}, где n_i – также доля голосов, полученных i-й партией или i-м кандидатом, а n₁ – доля голосов, полученных лидером. Данный индекс обладает теми же отмеченными выше свойствами, что и индекс Лааксо – Таагеперы. При этом легко определить вклад каждого кандидата (каждой партии) в полученную сумму. Вклад лидера всегда равен единице; если есть только два участника, то вклад второго будет равен отношению его результата к результату лидера[672].

Далее в таблицах 5.1–5.9 покажем примеры значений индексов Лааксо – Таагеперы и Голосова для выборов в различных странах и различных регионах и муниципальных образованиях Российской Федерации[673]. Также в этих таблицах для сравнения приведены число участвовавших в выборах кандидатов или партий и результат лидера (в процентах от числа голосов, поданных за всех кандидатов или за все партии). В тех случаях, когда выборы проводились в два тура, показаны результаты первого тура.

В таблице 5.1 приведены данные о последних (на конец 2015 года) президентских выборах в 24 странах[674], из которых четыре расположены в Западной, Центральной и Северной Европе, восемь – постсоциалистические государства Европы, шесть – бывшие республики СССР, четыре – латиноамериканские страны и две страны расположены в Восточной Азии.

Таблица 5.1. Значения эффективного числа кандидатов на выборах президентов зарубежных стран

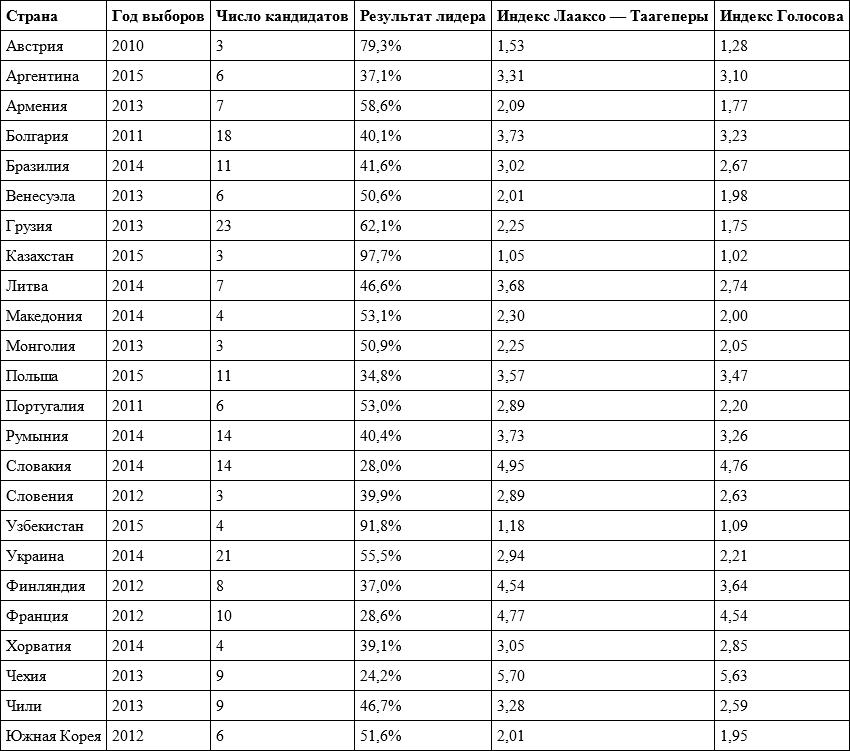
Как видно из таблицы, в половине случаев индекс Лааксо – Таагеперы превышал 3, а индекс Голосова – 2,5, что означает достаточно конкурентные выборы. Случаев же, когда индекс Лааксо – Таагеперы был ниже 2, а индекс Голосова – ниже 1,7, всего три – Казахстан, Узбекистан, где не было реальной конкуренции, а также Австрия, где полномочия президента весьма ограничены.

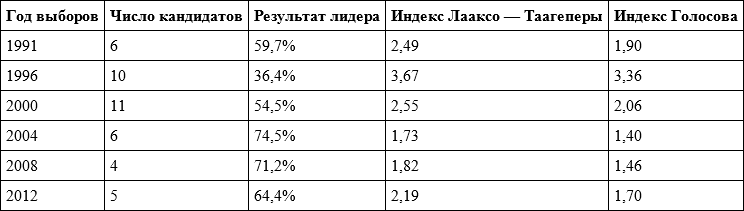
В таблице 5.2 приведены данные обо всех российских президентских выборах. Мы видим, что высококонкурентными были только выборы 1996 года, а в 2004 и 2008 годах индекс Лааксо – Таагеперы был ниже 2, а индекс Голосова – ниже 1,5.

Таблица 5.2. Значения эффективного числа кандидатов на выборах Президента Российской Федерации

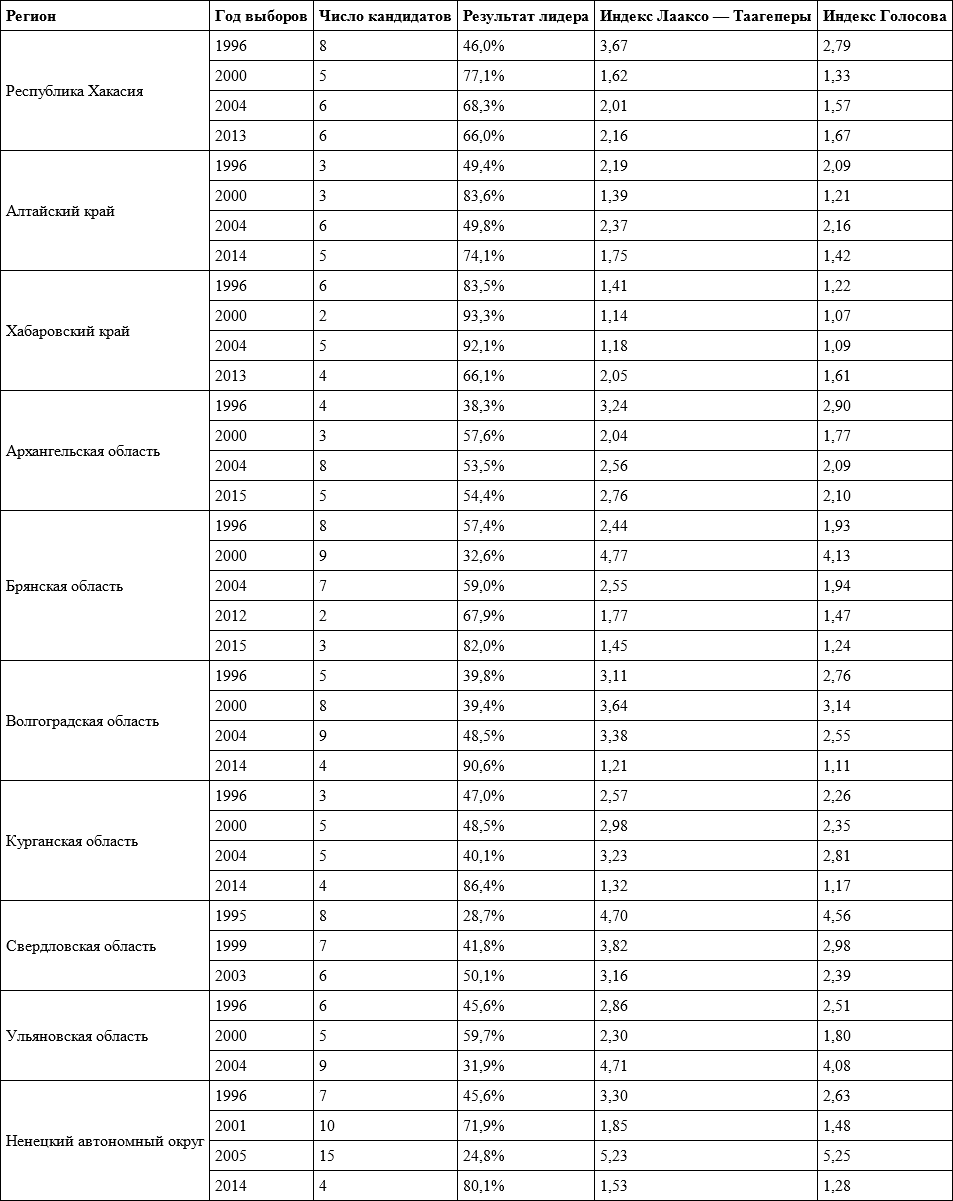
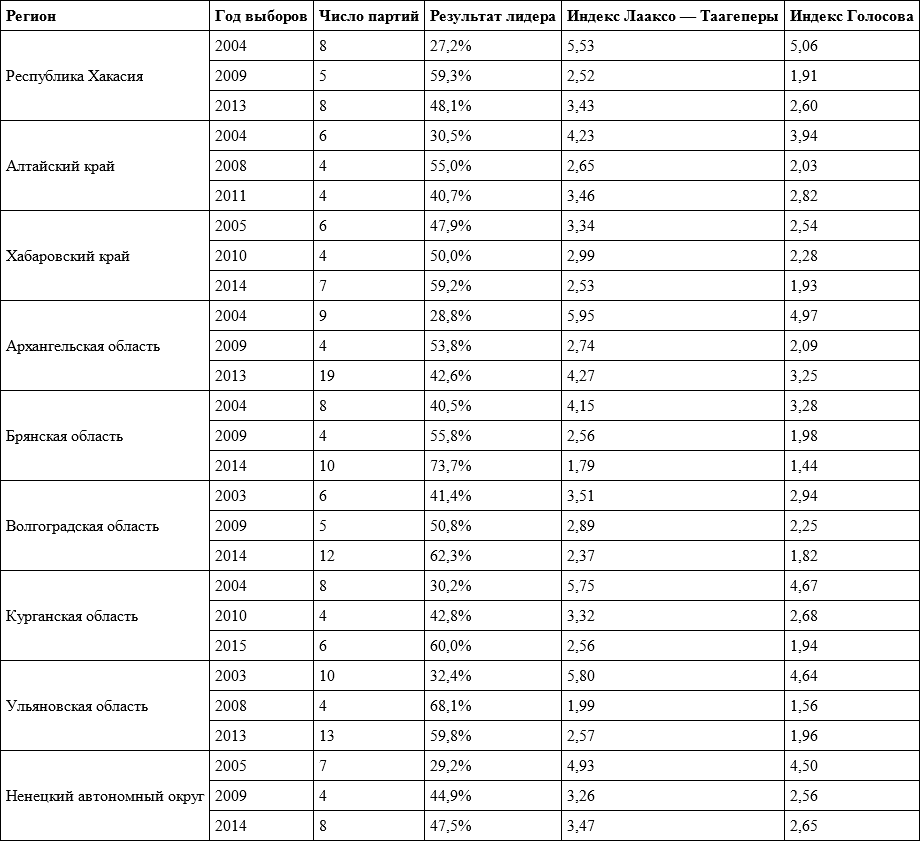
На выборах глав российских регионов разных лет ситуация в целом весьма пестрая. В таблице 5.3 приведены данные по 10 регионам, где такие выборы прошли не менее трех раз (чаще всего – четыре раза). Мы видим, что есть регионы с относительно высокой конкурентностью в течение всего периода (Архангельская область) и с крайне низкой (Хабаровский край). Однако для большинства регионов в разные годы индексы сильно различаются. Если же смотреть динамику, то нетрудно увидеть, что на выборах 1999–2000 годов конкуренция была в среднем ниже, чем в 1995–1996 годах, но в 2003–2005 годах она вернулась примерно на уровень 1995–1996 годов. После восстановления губернаторских выборов в 2012 году уровень конкуренции на них оказался заметно ниже, чем в 1990-х и 2000-х годах.

Таблица 5.3. Значения эффективного числа кандидатов на выборах глав российских регионов

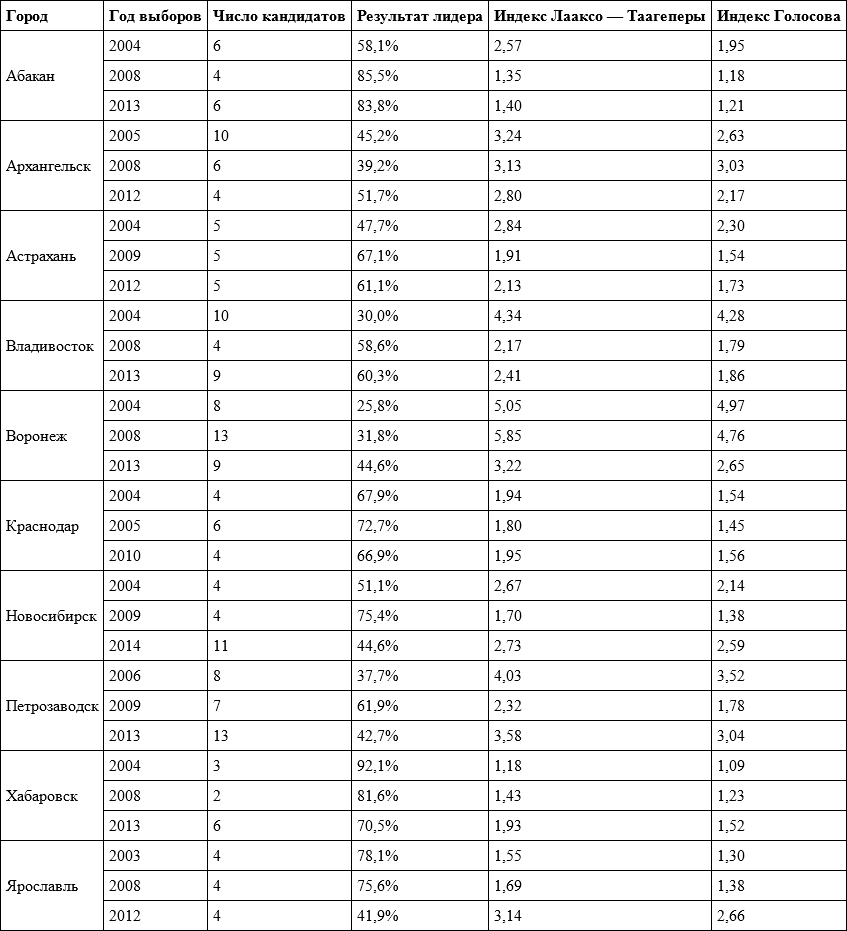
В таблице 5.4 приведены данные по выборам мэров 10 региональных центров, в каждом из которых за период 2003–2014 годов такие выборы прошли трижды. Здесь ситуация более ровная, чем на губернаторских выборах, и случаи крайне низкой конкуренции встречаются реже. Тем не менее заметно некоторое ослабление в среднем конкуренции в период 2008–2010 годов по сравнению с периодом 2003–2006 годов, а в период 2012–2014 годов произошел небольшой ее рост.

Таблица 5.4. Значения эффективного числа кандидатов на выборах глав российских городов

В таблице 5.5 приведены данные о последних (на ноябрь 2015 года) выборах 17 зарубежных парламентов[675]. Сравнивая их с данными таблицы 5.1, мы можем видеть, что конкуренция на парламентских выборах в основном выше, чем на президентских. Самая низкая степень конкуренции (индекс Голосова ниже 3, индекс Лааксо – Таагеперы ниже 3,4) из приведенных стран отмечается в Венгрии, Испании и Новой Зеландии. Крайне высокая степень партийной фрагментации в Бразилии, довольно высокая (значения индексов 7 и выше) в Израиле, на Украине и в Чехии.

Таблица 5.5. Значения эффективного числа партий на выборах парламентов зарубежных стран

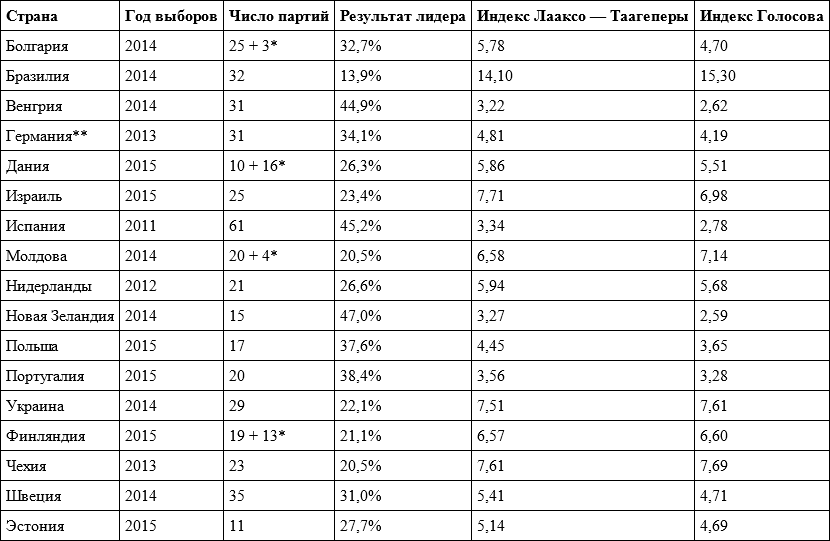
* Независимые кандидаты.

** ХДС и ХСС считались как две отдельные партии.

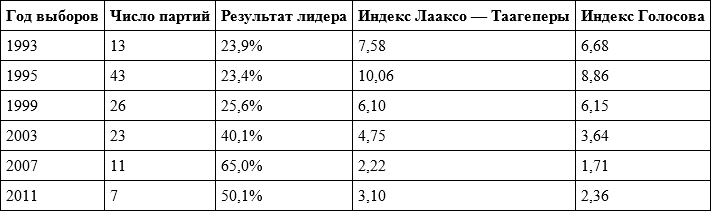
Обратившись к выборам в Государственную Думу (таблица 5.6), мы видим высокую степень партийной фрагментации в 1993 и особенно в 1995 году. Затем конкуренция и фрагментация снижались и достигли в 2007 году крайне низких значений. В 2011 году конкуренция несколько выросла, тем не менее значения обоих индексов оказались ниже, чем самые низкие значения этих индексов в таблице 5.5.

Таблица 5.6. Значения эффективного числа партий на выборах Государственной Думы

Из выборов региональных парламентов отдельное внимание стоит уделить Свердловской области, где пропорциональная система 8 раз использовалась для выборов нижней палаты Законодательного Собрания, а затем прошли выборы однопалатного Собрания по параллельной системе. Здесь картина похожая (см. таблицу 5.7). Самыми конкурентными были вторые выборы (1998 года), затем конкуренция в основном снижалась, достигнув минимума в 2008 году, после чего стала немного расти.

Таблица 5.7. Значения эффективного числа партий на выборах Законодательного Собрания Свердловской области

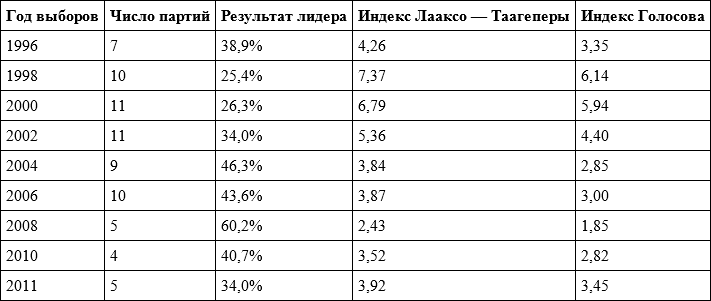
Примечание: 1996–2010 годы – выборы Областной Думы Законодательного Собрания по пропорциональной системе; 2011 год – выборы однопалатного Законодательного Собрания по параллельной системе.

В таблице 5.8 показаны данные о трижды прошедших выборах законодательных органов 9 регионов – тех же, что и регионы, для которых в таблице 5.3 приводились данные о губернаторских выборах (кроме Свердловской области). Как и там, в среднем наихудшей была конкуренция во втором цикле (2008–2010 годы).

Таблица 5.8. Значения эффективного числа партий на выборах российских региональных парламентов

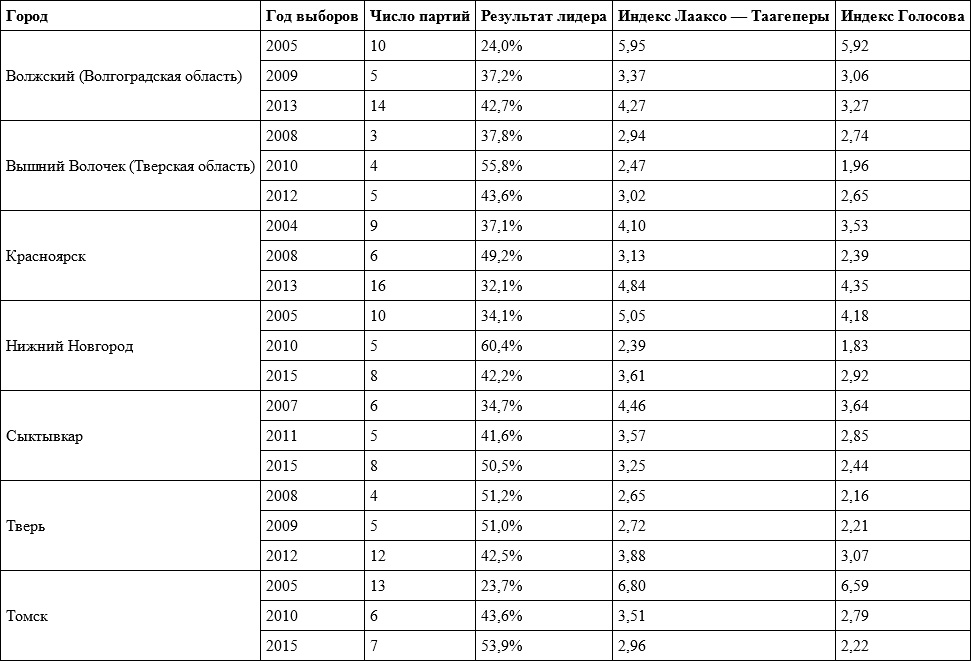
В таблице 5.9 приведены данные о трижды прошедших выборах по пропорциональной или параллельной системе представительных органов семи городов. Здесь также мы видим в основном более низкие значения индексов для 2008–2010 годов.

Таблица 5.9. Значения эффективного числа партий на выборах представительных органов российских городов

Всего в таблицах 5.1–5.9 приведены данные для 179 различных кампаний, и на их основе можно попробовать сделать некоторые обобщения. Очевидно, что оба индекса достаточно близки между собой, коэффициент корреляции между ними – 0,98. При этом в подавляющем большинстве случаев индекс Голосова ниже индекса Лааксо – Таагеперы. Обратных случаев всего 7, и все они относятся к высококонкурентным кампаниям, где их значения не ниже 5.

Корреляция обоих индексов с номинальным числом участников выборов хоть и значимая, но небольшая – 0,60–0,61. Гораздо выше (но, разумеется, со знаком минус) их корреляция с результатом лидера, она составляет –0,83 для индекса Лааксо – Таагеперы и –0,80 для индекса Голосова.