5.5. Методы выявления фальсификаций
Прежде чем обсуждать статистические методы выявления фальсификаций, следует обратить внимание на то, что фальсификации бывают разных видов. По своему влиянию на итоги голосования все способы фальсификаций можно разделить на три группы:
1) вброс – число голосов за одного кандидата (одну партию) увеличивается, а за других остается неизменным; в этом случае на число «вброшенных голосов» увеличивается показатель явки, то есть результат кандидата (партии) увеличивается формально за счет снижения числа не проголосовавших избирателей;
2) переброс – число голосов за одного кандидата (одну партию) увеличивается за счет снижения числа голосов за другого кандидата (другую партию);
3) изъятие – вид, противоположный вбросу – число голосов за одного кандидата (одну партию) уменьшается, а за других остается неизменным; в этом случае показатель явки также снижается, то есть результат кандидата (партии) уменьшается формально за счет повышения числа не проголосовавших избирателей.
Отметим, что в нашей практике случаи изъятия встречались существенно реже, чем случаи вброса и переброса.
Необходимо также различать способы фальсификаций в зависимости от того, на какой стадии избирательного процесса они произошли: на стадии голосования, подсчета голосов или подведения итогов голосования. В ходе голосования возможны лишь фальсификации типа вброса – это может быть как непосредственный вброс пачки бюллетеней в урну, так и многократное голосование одних и тех же лиц, незаконно получающих бюллетени. В ходе подсчета голосов в основном используется переброс, хотя возможны также вброс и изъятие. На последней стадии (оформление протоколов) возможны все три варианта и их комбинации[727].
В связи с этим важно понимать, что отдельные математические методы могут быть пригодны для выявления фальсификаций одного вида или способа и неэффективны в случае применения других способов.
Одним из наиболее простых и понятных методов выявления фальсификаций является сравнительный (дисперсионный анализ) – сравнение итогов голосования на близких по составу электората избирательных участках или территориях. Такое сравнение удобно осуществлять с помощью таблиц или, что более наглядно, с помощью гистограмм. Если электорат достаточно однородный, то при честном проведении голосования и подсчета голосов разброс не должен быть велик. Фальсификации же обычно осуществляются не по всем избирательным участкам[728], и это приводит к заметному увеличению разброса.
Различные примеры применения данного метода приведены в нашей работе[729]. Здесь мы ограничимся примером, когда на выборах, проходивших по смешанной несвязанной системе, были параллельно построены гистограммы итогов голосования в одном и том же городе за избирательный блок по федеральному округу и за лидера этого блока по одномандатному округу (иллюстрация 5.2). По этим гистограммам хорошо видно, насколько разброс доли голосов, поданных за кандидата, слабее разброса голосов, поданных за избирательный блок. В данном случае из первой гистограммы мы можем сделать вывод о достаточной однородности городского электората, и в сравнении с ней вторая гистограмма ясно указывает на фальсификацию итогов голосования по федеральному округу.
Более сложные методы выявления фальсификаций в России начали разрабатываться в начале 1990?х годов группой исследователей под руководством А. А. Собянина и В. Г. Суховольского. Одним из первых был предложен метод ранговых распределений, основанный на предположении, что при свободной конкуренции число голосов, получаемых кандидатами, должно удовлетворять закону Ципфа – Парето, который выражается следующим уравнением:
ln Ni = A – B * ln i,
где Ni – число голосов, полученных каждым кандидатом, i – место, полученное кандидатом в ходе выборов, A и B – константы, которые могут быть различными для каждых конкретных выборов.
Для проверки, удовлетворяют ли итоги голосования закону Ципфа – Парето, достаточно построить зависимость итогов голосования за каждого кандидата (в абсолютных или относительных величинах) от занятого им места в двойных логарифмических координатах: в случае удовлетворения эта зависимость должна ложиться с хорошей точностью на прямую линию.
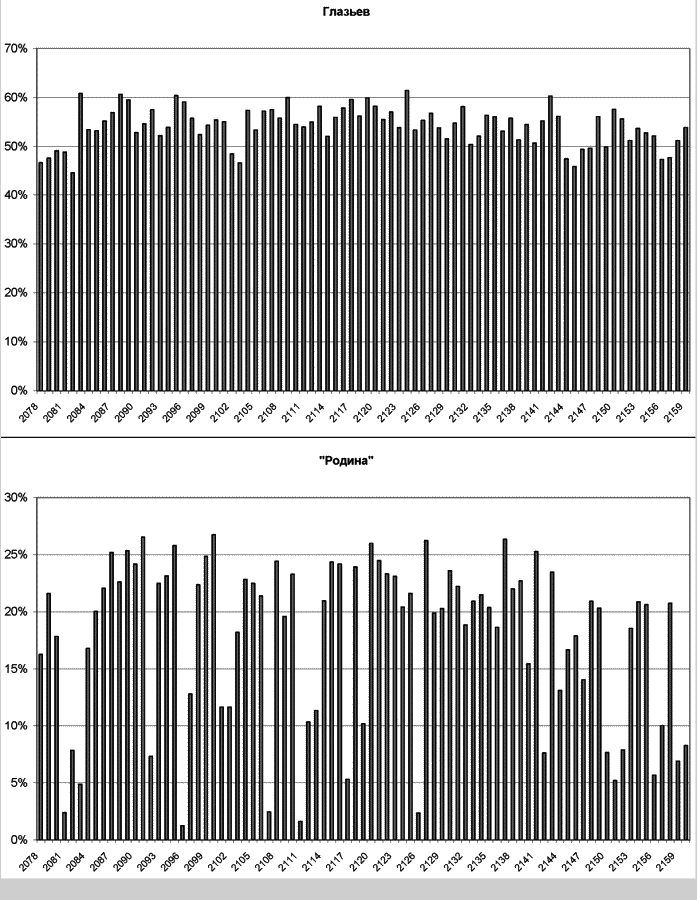
Иллюстрация 5.2. Итоги голосования в разрезе избирательных участков в г. Подольске (Московская область) на выборах депутатов Государственной Думы 2003 года за С. Ю. Глазьева по одномандатному округу (вверху) и за блок «Родина» по федеральному округу (внизу). Источник: Любарев А. Е., Бузин А. Ю., Кынев А. В. Мертвые души. Методы фальсификации итогов голосования и борьба с ними. М., 2007. С. 137
По утверждениям авторов метода, исследование большого массива данных о результатах выборов в разных странах, включая выборы в России в 1990–1991 годах, привело их к выводу, что в большинстве случаев закон Ципфа – Парето выполнялся. Этот метод был применен авторами для выявления фальсификаций в г. Кызыле на выборах Президента РСФСР 1991 года, а также на выборах губернатора Липецкой области 1993 года.
Однако при этом сами авторы отмечали, что нарушение данной закономерности может быть следствием не только прямых фальсификаций, но и других нарушений принципа свободной конкуренции. Более того, они отметили, что закон Ципфа – Парето будет выполняться тогда, когда каждый из кандидатов, каждая из партий обладает своей собственной, не перекрывающейся со всеми остальными политической платформой[730].
Ю. Н. Благовещенский и И. А. Винюков, анализируя данный метод на материале выборов депутатов Государственной Думы 2003 года, отметили, что в современных российских условиях при голосовании по партийным спискам картина оказывается более сложной. Есть группа лидеров, для которых закон Ципфа – Парето выполняется удовлетворительно, и группы середняков и аутсайдеров, для каждой из которых данный закон выполняется обычно хуже и с другими коэффициентами наклона (а потому для всех партий вместе закон Ципфа – Парето выполняется плохо)[731]. Получается, что конкуренция между разными партиями идет на разном поле: между лидерами – на одном, между середняками – на другом, между аутсайдерами – на третьем. Приходится делать вывод, что данный метод можно применять только для группы лидеров, и то с большой осторожностью.
В силу указанных обстоятельств метод ранговых распределений не получил сколько-нибудь широкого применения.
Другой метод был использован А. А. Собяниным и В. Г. Суховольским для доказательства фальсификаций на выборах депутатов Государственной Думы 1993 года. Он основан на предположении, что в отсутствии фальсификаций результаты кандидатов или партий (в процентах от числа проголосовавших избирателей или действительных голосов) не зависят от активности избирателей. Если же результаты кандидатов или партий на отдельных территориях (избирательный участок, район и т. п.) выражать в процентах от списочного числа избирателей, то зависимость таких результатов от показателя явки должна выражаться прямой, исходящей из начала координат, тангенс угла наклона которой равен среднему проценту голосов от числа проголосовавших избирателей.
Такие «нормальные» графики действительно часто наблюдаются на выборах (см. верхний график на иллюстрации 5.3). Однако встречаются и графики, которые с точки зрения данной гипотезы следует считать «аномальными»: в них точки, характеризующие итоги голосования на отдельных территориях, располагаются вдоль регрессионной прямой, пересекающей ось ординат заметно выше или ниже начала координат (см. нижний график на иллюстрации 5.3).
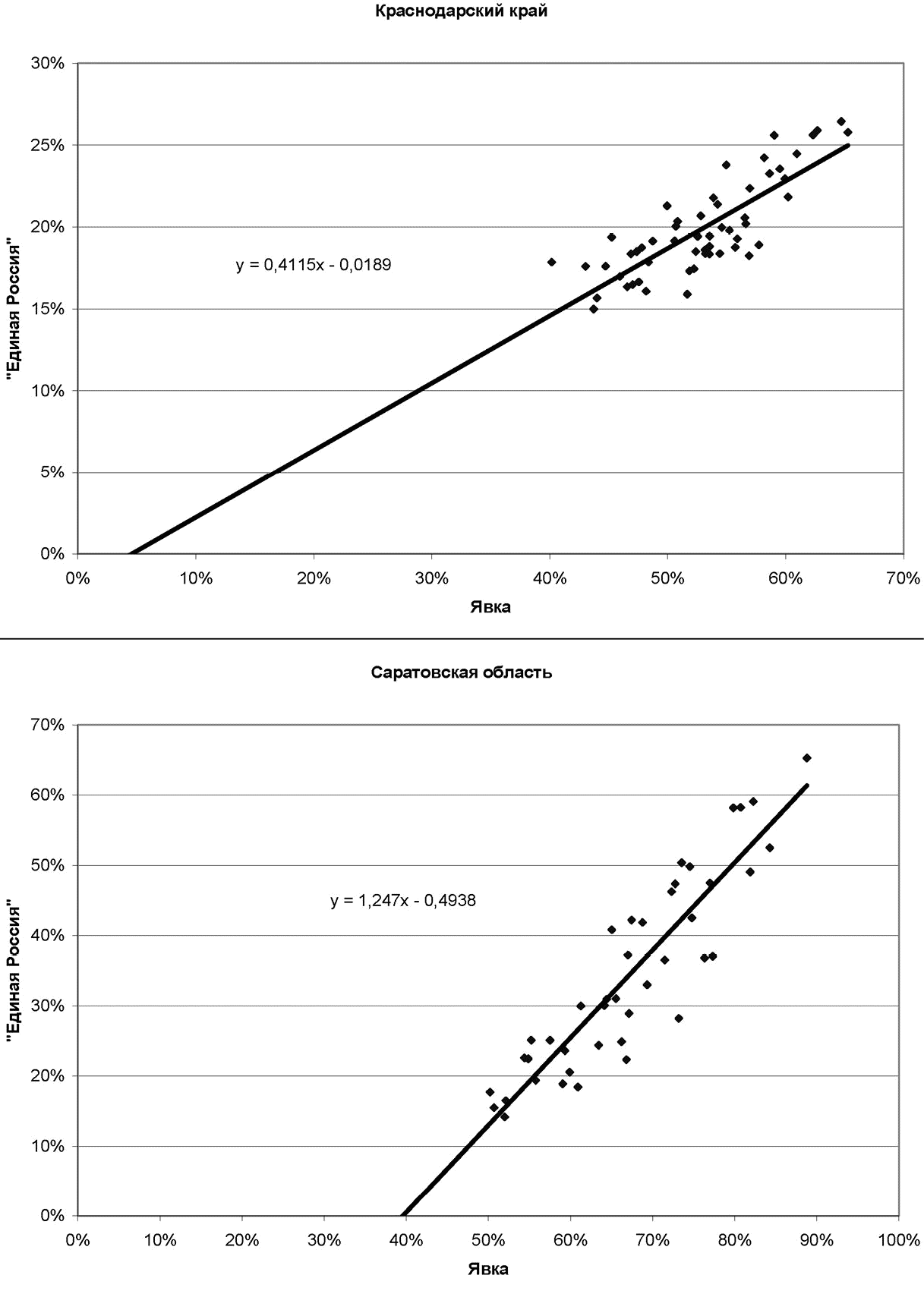
Иллюстрация 5.3. Зависимость доли голосов за «Единую Россию», выраженной в процентах от списочного числа избирателей, от явки в разрезе ТИК на выборах депутатов Государственной Думы 2003 года для Краснодарского края (вверху) и Саратовской области (внизу). Источник: Любарев А. Е., Бузин А. Ю., Кынев А. В. Мертвые души. Методы фальсификации итогов голосования и борьба с ними. М., 2007. С. 146
Особое внимание следует обратить на случаи, когда результаты одного кандидата ложатся на прямую, имеющую тангенс угла наклона, равный единице, а результаты остальных кандидатов (а также доля недействительных бюллетеней) ложатся на горизонтальные прямые. Это означает, что все «дополнительно пришедшие» (по сравнению с территориями с минимальной явкой) избиратели голосовали только за одного кандидата. По мнению авторов метода, такие графики свидетельствуют о фальсификациях типа вброса[732].
Аналогичный метод применял позднее В. В. Михайлов для выявления фальсификаций на выборах в Татарстане и других российских регионах 1991–2001 годов. Однако он по оси ординат откладывал долю голосов от числа проголосовавших избирателей. В таком варианте «нормальные» линии должны были иметь нулевой наклон, а «аномальные» – положительный для кандидата, в пользу которого совершались фальсификации, и отрицательный для остальных[733]. Однако такой способ анализа не позволяет отличать «нормальный» случай от случаев, когда закономерности не видно из-за сильного разброса: в обоих случаях коэффициент корреляции будет близок к нулю. При способе Собянина – Суховольского в «нормальном» случае коэффициент корреляции будет близок к единице.
Метод корреляции с явкой Собянина – Суховольского был развит в работах М. Мягкова, Д. Шакина и соавторов, посвященных анализу выборов в России и на Украине. Тангенс угла наклона кривой на графиках Собянина – Суховольского (один из двух параметров регрессионного уравнения) они назвали «поддержкой дополнительных избирателей» (ПДИ) и в качестве критерия отклонения от «нормы» (нерегулярности в их терминологии) использовали разность между ПДИ и результатом кандидата (партии) относительно числа проголосовавших избирателей[734].
Мы в своей работе использовали в основном другой показатель – второй параметр регрессионного уравнения, то есть отрезок, отсекаемый регрессионной прямой на оси ординат. Этот параметр мы назвали смещением регрессионной линии (СРЛ). В идеальном случае значение СРЛ должно быть нулевым (то есть регрессионная линия должна попадать в начало координат). По нашим оценкам, «нормальными» можно считать итоги голосования, при которых значение СРЛ по модулю не превышает 0,1 (или 10 %). Превышение этого порога свидетельствует об аномалиях[735].
Метод корреляции с явкой Собянина – Суховольского неоднократно подвергался критике. Главные аргументы оппонентов сводятся к тому, что гипотеза о независимости голосования и явки может не выполняться не только из-за прямых фальсификаций, но и по другим причинам. При этом можно выделить три альтернативных объяснения.
Первое сводится к тому, что помимо прямых фальсификаций возможны и некоторые незаконные формы воздействия на избирателей, которые могут приводить к подобным эффектам – давление на избирателей, контроль за их волеизъявлением[736]. Однако такие незаконные действия можно объединить с фальсификациями в одну группу, и в этом случае аномалии, выявляемые методом корреляции с явкой, будут мерилом более широкого явления – использования административного ресурса в процессе голосования и подведения его итогов.
Второе объяснение основано на представлении, согласно которому различные категории избирателей отличаются не только своими политическими предпочтениями, но и активностью на выборах. В наиболее общем виде его можно сформулировать так: конформистски настроенные группы избирателей (сельский электорат, лица пожилого возраста) показывают повышенную активность на выборах и одновременно повышенный уровень поддержки представителей власти и (или) традиционных политических сил.
Третье объяснение предполагает, что кандидаты и партии, поддержка которых растет с явкой, просто более активно работали с теми группами избирателей, которые колебались в своем выборе, в том числе и в выборе «голосовать – не голосовать». В результате именно они привели на выборы этих колебавшихся избирателей, и потому корреляция их поддержки с явкой вполне закономерна.
Следует отметить, что во многих критических высказываниях заметно непонимание разницы между различиями итогов голосования во времени (то есть между выборами, проводившимися в разные даты) и в пространстве (то есть между разными территориями на одних и тех же выборах). Так, отмечалось, что при низкой явке в России в 1990-е годы доля голосов за левых была выше, чем на выборах с высокой явкой[737] (то же самое наблюдалось в 2000-е годы в отношении голосования за партию власти). Однако если бы эта закономерность распространялась на пространственные различия, то зависимость голосования от явки для левых (или за власть) имела бы пониженный наклон, а за правых – повышенный. На самом деле наблюдалась противоположная картина.
Проанализировав большой массив электоральной статистики на российских выборах 1991–2008 годов, мы смогли сделать следующие выводы. Во-первых, оказалось, что «нормальный» характер связи между явкой и поддержкой кандидатов или партий был вплоть до середины 2000-х годов характерен для городского электората. Для сельских районов и регионов с высокой долей сельского населения «аномальные» результаты получались достаточно часто, и потому можно было бы предположить, что такие результаты характерны для сельского электората. Однако мы увидели, что и для ряда сельских районов получались вполне «нормальные» результаты. Поэтому остается вопрос: действительно ли «аномалии» получались вследствие особенностей самого сельского электората, или они связаны с тем, что в сельской местности и до середины 2000-х годов в широких масштабах практиковались фальсификации либо иные незаконные способы воздействия на итоги голосования?
Во-вторых, «аномальность» в значительной степени зависела от силы региональной власти и ее заинтересованности в результатах выборов. Кроме того, наиболее «аномальные» результаты получались именно в тех регионах, из которых было больше всего обоснованных сообщений о фальсификациях.
Проверяли мы и предположение о том, что кандидаты и партии, поддержка которых росла с явкой, более активно работали с теми группами избирателей, которые колебались в своем выборе. Такая активность действительно иногда приводила к небольшим «аномалиям», но нигде в подобных случаях значение ПДИ не приближалось к единице.
В 2007–2008 годах степень «аномальности» в городах (включая Москву) резко выросла. И это не может быть объяснено иначе как массовыми фальсификациями[738].
В цитированных выше работах М. Мягкова и соавторов был использован также метод исследования распределения явки[739]. Впоследствии этот же метод был предложен С. Шпилькиным в ходе анализа федеральных выборов 2007–2008 годов[740], затем он неоднократно использовался А. Ю. Бузиным[741].
Метод заключается в построении графика, где по оси абсцисс откладывается явка, а по оси ординат – число избирательных участков, на которых явка укладывается в соответствующий однопроцентный интервал, точнее полуинтервал (например, для явки 50 % это от 49 до 50 % или от 50 до 51 %), либо число избирателей на таких участках, либо их доля. Метод может быть использован для территорий, содержащих значительное число участков (две-три тысячи и более), для меньших территорий приходится использовать двух– или даже пятипроцентные интервалы, но точность и наглядность в этом случае значительно ниже.
По мнению исследователей, использующих данный метод, на относительно однородных территориях при отсутствии административного воздействия получающиеся кривые распределения должны быть близки к гауссовым, то есть иметь один «горб» и быть достаточно симметричными. При этом опыт показывает, что требование однородности может быть существенно смягчено. Важно лишь, чтобы состав электората менялся от одной крайности к другой достаточно плавно. Так, в существенно неоднородной России на федеральных выборах 1995–2003 годов получались вполне «нормальные» кривые распределения – с одним четко выраженным пиком и несильными отклонениями от симметрии (а при исключении республик они становились еще более симметричными)[742].
Применение данного метода удобнее всего проиллюстрировать на примере Москвы. Во-первых, в Москве вполне однородный электорат. Во-вторых, здесь достаточное количество избирательных участков – более трех тысяч. В-третьих, по данным многолетних наблюдений и исследований, уровень фальсификаций в Москве имел четкую динамику: до 2003 года они практически не наблюдались, в 2004 и 2005 годах носили локальный характер, в 2007 году уровень фальсификаций стал существенными, а в 2008, 2009 и 2011 годах – очень высоким. Затем, после массовых протестов, в 2012, 2013 и 2014 годах уровень фальсификаций вновь снизился почти до нуля[743].
На иллюстрации 5.4 показаны кривые распределения явки по Москве для 7 из 11 федеральных и общегородских кампаний, проходивших с 2000 по 2014 год. Как видно из графика, отмеченная выше динамика уровня фальсификаций четко отражается на кривых распределения. Кривая для президентских выборов 2000 года почти идеальна, и на президентских выборах 2012 года получилась точно такая же кривая, лишь смещенная в сторону более низких значений явки. Также близки к идеальным кривые для выборов в Московскую городскую Думу 2014 года и выборов мэра Москвы 2013 года (последняя на графике не показана). Кривые для выборов Президента РФ 2004 года (не показана), в Московскую городскую Думу 2005 года и в Государственную Думу 2007 года также имеют один основной «горб», но на них уже видны искажения. А вот кривые для выборов Президента РФ 2008 года (не показана), выборов в Московскую городскую Думу 2009 года и в Государственную Думу 2011 года вообще не имеют выраженного основного пика; они «размазаны» в широком диапазоне значений явки, но при этом имеют небольшие локальные пики – в основном на «круглых» значениях явки (40, 50, 55, 60, 65, 75 %).
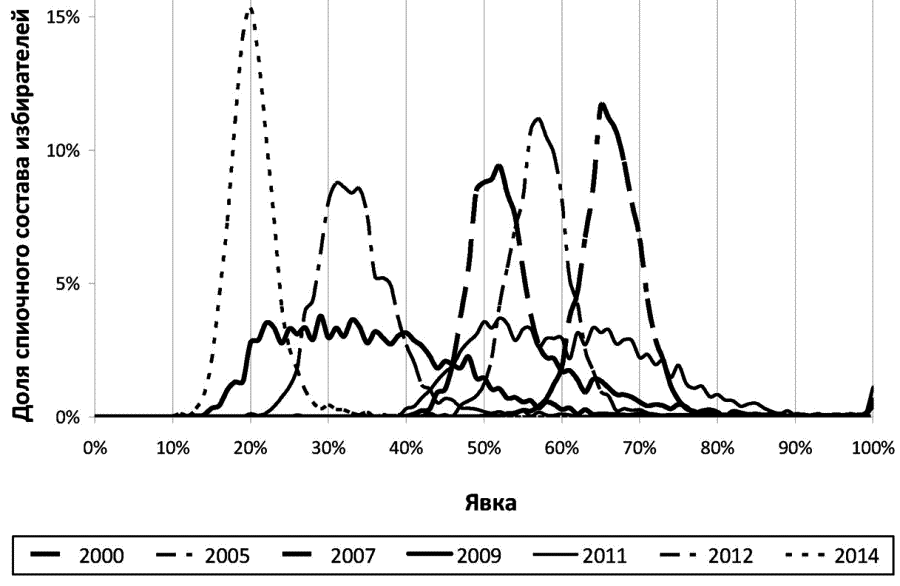
Иллюстрация 5.4. Кривые распределения явки для различных федеральных и общегородских выборов на территории Москвы (построены на основе расчетов А. Ю. Бузина)
Очевидно, поведение электората не может так резко меняться в течение короткого времени, а активность однородного городского электората не может описываться пилообразными кривыми распределения. И эти данные являются дополнительным свидетельством административного воздействия на итоги голосования в период 2008–2011 годов.
Синтезом методов корреляции с явкой Собянина – Суховольского и метода исследований распределения явки можно считать метод, который был разработан С. Шпилькиным в 2008 году[744]. В данном случае также строятся кривые распределения по однопроцентным интервалам явки, но по оси ординат откладываются число или доля голосов, поданных за кандидатов или партии. Как и в случае распределения явки, метод применим для территорий с большим количеством избирательных участков.
Идея метода основана, как и у Собянина и Суховольского, на предположении о независимости голосования и явки. Однако несомненное достоинство метода Шпилькина заключается в наличии внутреннего контроля. Как было показано автором метода на примере российских федеральных выборов 2007 и 2008 годов, кривые для всех партий (для выборов 2007 года) или для всех кандидатов (для выборов 2008 года), кроме лидеров («Единой России» и Д. А. Медведева соответственно), были фактически подобны, то есть представляли одну и ту же зависимость с разными множителями. Такое подобие и является свидетельством независимости результата от явки. Более того, кривые для лидеров тоже были подобны остальным – но только на восходящем участке, то есть в области низких значений явки, а на нисходящем участке (то есть в области высоких значений явки) они шли выше (см. иллюстрацию 5.5); иными словами, в терминологии Шпилькина, в дополнение к «нормальным» голосам лидер получал еще и «аномальные».
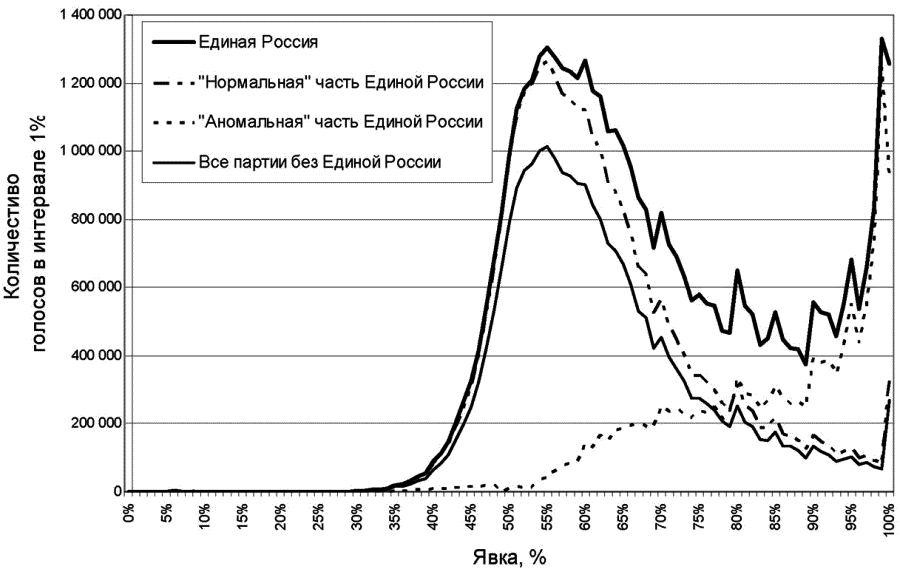
Иллюстрация 5.5. Разделение голосов за «Единую Россию» на выборах 2007 года на «нормальную» и «аномальную» части. Источник: Бузин А. Ю., Любарев А. Е. Преступление без наказания: Административные избирательные технологии федеральных выборов 2007–2008 годов. М., 2008. Илл. 38 (иллюстрация предоставлена С. А. Шпилькиным)
Другим важным достоинством метода Шпилькина является возможность на основании построенных зависимостей оценить количество «аномальных» голосов. Для этого строится зависимость суммы голосов за всех кандидатов (или все партии), кроме лидера. Затем определяется подгоночный коэффициент, на который умножается это «суммарное» распределение. Данный коэффициент вычисляется таким образом, чтобы восходящая ветвь «нормальной» составляющей как можно более плотно прилегала к восходящей ветви кривой распределения для лидера. В результате получается кривая распределения «нормальных» голосов за лидера, а разность между фактическим распределением и «нормальным» и дает в результате интегрирования количество «аномальных» голосов.
В результате применения данного метода число «аномальных» голосов на выборах в Государственную Думу 2007 года было оценено в 13,8 млн голосов, на выборах Президента РФ 2008 года – в 14,8 млн голосов[745], на выборах в Государственную Думу 2011 года – в 15,3 млн голосов[746], а на выборах Президента РФ 2012 года – в 11,0 млн голосов[747].
Отметим, что метод Шпилькина, как и метод корреляции с явкой Собянина – Суховольского, эффективен для выявления фальсификаций типа вброса и малопригоден для выявления перебросов.
Принципиально другой подход используют методы, основанные на анализе частоты появления в официальных протоколах избирательных комиссий различных цифр. Смысл этих методов в том, что при составлении протоколов на основе истинных итогов голосования, выявленных путем подсчета голосов, цифры должны распределяться в них случайным образом. Если же протоколы «корректируются», то в силу психологических факторов некоторые цифры в них начинают появляться чаще, а другие – реже. Таким образом, эти методы позволяют выявлять фальсификации на последних стадиях подведения итогов голосования, в том числе и переброс.
Подобный подход использовали У. Мебейн и К. Калинин. Они анализировали распределение в протоколах второй значащей цифры, которое должно подчиняться «закону Бенфорда для второй значащей цифры» (округленно для цифр от 0 до 9 частота соответственно 0,120; 0,114; 0,109; 0,104; 0,100; 0,097; 0,093; 0,090; 0,088; 0,085). Отклонение распределения от этого закона трактуется ими как признак фальсификаций[748].
Существуют также методы, основанные на проверке частот появления различных цифр в младших разрядах чисел. Однако их применимость для анализа искажений результатов голосования подвергается сомнению[749].
Существуют также методы, которые могут быть применены в особых случаях. Так, если выборы проводились в два тура, полезно сравнение итогов голосования в первом и втором турах. Например, В. В. Михайлов, анализируя результаты выборов Президента РФ 1996 года, использовал коэффициент переориентации избирателей, получаемый делением отношения числа голосов, полученных в первом туре кандидатами, вышедшими во второй тур, на отношение голосов, полученных этими кандидатами во втором туре. Михайлов показал, что данный коэффициент мало отличался для большинства регионов, несмотря на их существенные различия в уровне голосования за основных кандидатов. В тех же регионах или территориях, где коэффициент переориентации избирателей существенно отличался от среднего, были основания подозревать фальсификации во втором туре[750].
М. Мягков и соавторы предложили еще один метод анализа для двухтуровых выборов. Используя статистические методы для оценки перетока голосов (см. подраздел 5.4.2), они постулировали, что получаемые результаты, выражаемые в долях перетока, не должны быть выше 1 (100 %) и ниже 0. Любой выход значений за пределы этого диапазона свидетельствует о «нерегулярностях», а величина превышений дает численную оценку числа «нерегулярных» голосов[751].
В тех случаях, когда на части территории выборы проходят с использованием технических средств, а на другой части – обычным способом, полезно сравнить между собой результаты, полученные на этих частях. Хотя применение технических средств (например, Комплексов обработки избирательных бюллетеней) не может полностью исключить возможности фальсификаций, оно блокирует применение наиболее легких способов фальсификации, таких как вброс прачки бюллетеней в стационарную урну, неправильный подсчет голосов и неправильное составление протокола. Поэтому итоги голосования на участках, оборудованных такими Комплексами, могут в первом приближении рассматриваться как честные[752]. Правда, оснащение участков техническими средствами обычно не является случайным, поэтому важно для контроля проверить итоги голосования на тех же участках на других выборах, где эти средства не использовались, и сделать соответствующую коррекцию. Примеры таких расчетов приведены в наших работах[753].
Могут использоваться также другие методы, такие как сравнительный анализ данных протоколов по разным видам голосования (при совмещении выборов, а также при смешанной системе с двумя бюллетенями), корреляция между определенными результатами, проверка контрольных соотношений, которые должны выполняться, но не предусмотрены законом, и т. п.[754].
В заключение этого раздела заметим, что любые статистические методы не являются и не могут являться юридическим доказательством фальсификаций. Однако, по нашему глубокому убеждению, результаты, полученные надежными статистическими методами, могут и должны приниматься правоприменительными и правоохранительными органами (избирательными комиссиями, прокуратурой, судом) в качестве оснований для проведения проверок на предмет фальсификаций и иных нарушений избирательного законодательства. Кроме того, статистические методы могут использоваться для оценки масштаба фальсификаций в тех случаях, когда факты фальсификаций выявлены и нужно решить, могли ли они повлиять на результаты выборов[755].
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК